March 2018 – Optimization in Machine Learning

AdaGrad

AdaGrad is simply just an optimization method based off of the Proximal Point Algorithm (otherwise known as the Gradient Descent algorithm), specifically the Stochastic version of gradient descent. The intention behind the formulation of AdaGrad is because SGD (stochastic gradient descent) converges slowly in the cases when features of our model are significantly more important than others. This is because the original SGD algorithm treats all factors equally, regardless of how much each factor contributes towards the actual models outputs.

Seen below, we can recognize that the stochastic gradient descent algorithm takes a large amount of time in order to find the optimal solution because of the constant jumping back and forth on the expected gradient (seen Left). On the otherhand, if we were to average all of the iterates in SGD (not AdaGrad), we can find a much quicker optimization and decrease the amount of backtracking done.

Now consider a case where we have an extremely wide problem domain, most likely due to a feature having an exaggerated effect on the domain. Seen below, we can see that the standard proximal gradient method (SGD) ends up jumping back and forth because it is a poorly conditioned problem. On the other hand, we can see the AdaGrad variant (which somewhat fixes the poor conditioning of the problem) will end up getting to the optimal in a significantly smaller number of steps.

The original SGD algorithm’s update method defines the update rule as:

$x^{(k+1)} = \text{argmin}_{x \in \chi} \{ \langle g^{(k)}, x \rangle + \frac{1}{2 \alpha_k} \lvert \lvert x - x^{(k)} \rvert \rvert_2^2 \}$

This version of the algorithm has a general convergence rate of $O(1/\sqrt{T})$

AdaGrad takes advantage of the matrix norm, in our case, $B$ will be a positive definite matrix such that:

$\lvert \lvert x \rvert \rvert^2_B := x^T Bx \geq 0$

This matrix $B$ has a list of diagonal terms that will modify the update rule of SGD such that:

$x^{(k+1)} = \text{argmin}_{x \in \chi} \{ \langle \nabla f(x^{(k)}), x \rangle + \frac{1}{2 \alpha_k} \lvert \lvert x - x^{(k)} \rvert \rvert_B^2 \}$

which is equivalent to an update rule of:

$x^{(k+1)} = x^{(k)} - \alpha B^{-1} \nabla f(x^{(k)})$

As can be seen when compared to the original update rule, we have introduced the diagonal matrix $B$ in order to converge more quickly because of the reliance on features that are more exaggerated than less important features. Now the question is how we can best approximate $B$, since it is unknown to the user.

AdaGrad now extends the SGD algorithm by defining within iteration $k$ :

$G^{(k)} = \text{diag} \lbrack \sum_{i=1}^{k} g^{(i)} (g^{(i)})^T \rbrack^{1/2}$

We can define $G^{(k)}$ as a diagonal matrix with entries:

$G^{(k)}_{jj} = \sqrt{\sum_{i=1}^{k} (g_j^{(i)})^2}$

Therefore modifying our previous modified update rule to be our final update rule for Adagrad:

$x^{(k+1)} = \text{argmin}_{x \in \chi} \{ \langle \nabla f(x^{(k)}), x \rangle + \frac{1}{2 \alpha_k} \lvert \lvert x - x^{(k)} \rvert \rvert_{G^{(k)}}^2 \}$

which is equivalent to an update rule of:

$x^{(k+1)} = x^{(k)} - \alpha G^{-1} \nabla f(x^{(k)})$

Proof of Convergence:

In order to go about proving that this new update rule will converge on the optimal solution just as SGD does, we must go about looking at the logic behind our choosing the diagonal matrix for our value of the matrix $B$.

To go about proving this we must have a couple of initial assumptions, definitions, and observations:

Assumption 1

$\vert \lvert x - x^{*} \rvert \rvert_{\infty} \leq R_{\infty}$ for all $x \in \chi$

Definition 1

(bound on the second moments of the $j$ th partial derivative of the function $F$ )

$\sigma_j^2 \geq E\lbrack (\nabla_j F(x;a_i))^2 \rbrack$ for all $x \in \chi$

Observation 1

$C \subset R^n$

$\pi_C^A (y) := \text{argmin}_{x \in C} \lvert \lvert x-y \rvert \rvert^2_A$

for any $x \in C$ then:

$\lvert \lvert \pi_C^A (y) - x \rvert \rvert^2_A \leq \lvert \lvert y - x \rvert \rvert^2_A$

Observation 2

$f$ is convex and differentiable such that:

$f(y) \geq f(x) + \langle f(x), y-x \rangle$

We utilize a theorem defined in the original paper which is also proved later on in the paper that suggests that given a step-size $\alpha = R_\infty$ and $\hat{x}_k = \frac{1}{k} \sum_{k=1}^{K} x_k$ such that:

Theorem 3

$E \lbrack f(\hat{x}_k) \rbrack - f(x^*) \leq \frac{2 R_\infty}{K} \sum_{j=1}^{n} E \lbrack ( \sum_{k=1}^{K} g_{k,j}^2 )^{1/2} \rbrack \leq 2 \frac{R_\infty \sum_{j=1}^{n} \sigma_j}{\sqrt{K}}$

The above equation is what we want to end up proving in order to show that the AdaGrad algorithm will converge on an optimal solution given enough steps $k$ .

Proof

Now that we’ve gone about and defined all of our required values, we can go about proving the convergence of the AdaGrad algorithm.

We first look at our update step of:

$x_{k+1} = \text{argmin}_{x \in \chi} \{ \langle g_k, x \rangle + \frac{1}{2\alpha} \lvert \lvert x - x_k \rvert \rvert^2_{G_k} \}$

which when projected into our problem space:

$\tilde{x}_{k+1} = x_k - \alpha G_K^{-1} g_k$

such that our new update step can be:

$x_{k+1} = \text{argmin}_{x \in \chi} \{ \lvert \lvert \tilde{x}_{k+1} - x \rvert \rvert^2_{G_k} \}$

This can be seen that the Potential Function is:

$\frac{1}{2} \lvert \lvert x_k - x^* \rvert \rvert^2_2$

And the AdaGrad Function would then be:

$\frac{1}{2} \lvert \lvert x_{k+1} - x^* \rvert \rvert^2_{G_k}$

Here, we’ll modify our AdaGrad function utilizing the previous definitions and the Potential function:

$\frac{1}{2} \lvert \lvert x_{k+1} - x^* \rvert \rvert^2_{G_k} \leq \frac{1}{2} \lvert \lvert x_k - \alpha G_k^{-1} g_k - x^* \rvert \rvert^2_{G_k}$

$= \frac{1}{2} \lvert \lvert \tilde{x}_{k+1} - x \rvert \rvert^2_{G_k}$

$= \frac{1}{2} \lvert \lvert x_k - x^* \rvert \rvert^2_{G_k} + \alpha \langle g_k, x^* - x_k \rangle + \frac{\alpha^2}{2} \lvert \lvert G_k^{-1} g_k \rvert \rvert^2_{G_k}$

$= \frac{1}{2} \lvert \lvert x_k - x^* \rvert \rvert^2_{G_k} + \alpha \langle g_k, x^* - x_k \rangle + \frac{\alpha^2}{2} \lvert \lvert g_k \rvert \rvert^2_{G_k^{-1}}$

We can see that the middle term of the final equation can be seen as:

$\langle g_k, x^* - x_k \rangle \leq f_k(x^*) - f_k(x_k)$

This rightmost term can be modfied to be:

$f_k(x^*) - f_k(x_k) \leq \frac{1}{2 \alpha} \lbrack \lvert \lvert x_k - x^* \rvert \rvert^2_{G_k} - \lvert \lvert x_k - \alpha G_k^{-1} g_k - x^* \rvert \rvert^2_{G_k} \rbrack + \frac{\alpha}{2} \lvert \lvert g_k \rvert \rvert^2_{G_k^{-1}}$

We can now modify this step with a summation of elements such that:

$\sum_{k=1}^{K} f_k(x^*) - f_k(x_k) \leq \frac{1}{2 \alpha} \sum_{k=1}^{K} \lbrack \lvert \lvert x_k - x^* \rvert \rvert^2_{G_k} - \lvert \lvert x_{k+1} - x^* \rvert \rvert^2_{G_k} \rbrack + \frac{\alpha}{2} \sum_{k=1}^{K} \lvert \lvert g_k \rvert \rvert^2_{G_k^{-1}}$

With this step, we can define $G_{k+1} \succeq G_k$ for all $k$ given that $G_k := \text{diag} (\sum_{i=1}^{K} g_i g_i^T)^{1/2}$ . With this definition we can now create a new Lemma:

$\sum_{k=1}^{K} \langle g_k, G_k^{-1} g_k \rangle \leq 2 \sum_{j=1}^{n} \sqrt{\sum_{k=1}^{K} g_{k,j}^2}$

Since we’ve expanded out our summation of elements above, we need to reduce our first term on the right side of the $\leq$ sign:

$\sum_{k=1}^{K} \lbrack \lvert \lvert x_k - x^* \rvert \rvert^2_{G_k} - \lvert \lvert x_{k+1} - x^* \rvert \rvert^2_{G_k} \rbrack = \lbrack \lvert \lvert x_1 - x^* \rvert \rvert^2_{G_1} - \lvert \lvert x_{k+1} - x^* \rvert \rvert^2_{G_k} \rbrack + \sum_{k=2}^{K} \lbrack \lvert \lvert x_k - x^* \rvert \rvert^2_{G_k} - \lvert \lvert x_{k} - x^* \rvert \rvert^2_{G_{k-1}} \rbrack$

The final term in the above equation is based off of the definitions of the norm and applying out when $G_k - G_{k-1}$ is needed to expand out our summation terms.

We use the basic definition of our space and the diagonal to form the defintion:

$\lvert \lvert y \rvert \rvert^2_{G_k} \leq \lvert \lvert \text{diag} (G_k) \rvert \rvert_1 \lvert \lvert y \rvert \rvert^2_\infty$

We use this definition in the final term of the previous equation that was expanded out in order to see that:

$\sum_{k=2}^{K} \lvert \lvert \text{diag}( G_k - G_{k-1} )\rvert \rvert_{1} \lvert \lvert x_{k} - x^* \rvert \rvert^2_\infty \leq \sum_{k=2}^{K} \lvert \lvert \text{diag}( G_k - G_{k-1} )\rvert \rvert_{1} R^2_\infty$

For better understanding we will define a new function:

$\text{tr} (X) = \lvert \lvert \text{diag} (X_k - X_{k-1}) \rvert \rvert_1$

Using the Assumption 1 we can now see that:

$\sum_{k=1}^{K} \lbrack \lvert \lvert x_k - x^* \rvert \rvert^2_{G_k} - \lvert \lvert x_{k+1} - x^* \rvert \rvert^2_{G_k} \leq R_\infty^2 \text{tr} (G_k) = R_\infty^2 \sum_{j=1}^{n} \sqrt{\sum_{k=1}^{K} g_{k,j}^2}$

Going back to one of our previous definitions, we can reduce this to:

$\sum_{k=1}^{K} f_k(x^*) - f_k(x_k) \leq \lbrack \frac{1}{2 \alpha} R_\infty^2 + \alpha \rbrack \sum_{j=1}^{n} \sqrt{\sum_{k=1}^{K} g_{k,j}^2}$

Given the fact that the potential function $E \lbrack f(x_k) | x_k \rbrack = f(x_k)$ we can now finally modify this to find our convergence proof that we were originally looking for:

$E \lbrack f(\hat{x}_k \rbrack - f(x^*) \leq \frac{1}{k} \lbrack \frac{1}{2 \alpha} R_\infty^2 + \alpha \rbrack E \lbrack \sum_{j=1}^{n} \sqrt{\sum_{k=1}^{K} g_{k,j}^2} \rbrack$

This proves that our given new update rule for AdaGrad will produce an optimal solution at (approximately) the same rate that SGD does.

Understanding Bayesian Optimization

The Prior and its Possibilities

I discussed Bayesian optimization, which is a way of optimizing a function that does not have a formula but can be evaluated. Bayesian optimization use Bayesian inference and thus have prior, likelihood, and posterior distributions. Bayesian optimization can be used to optimize hyperparameters in machine learning. Given a data set for learning on, the hyperparameters are the input to a function. The output to the function is some assessment of the machine learning model’s performance on the data such as F1-score, precision and recall, accuracy, and so on.

The following links were used in my understanding of Bayesian optimization:

PRACTICAL BAYESIAN OPTIMIZATION OF MACHINE LEARNING ALGORITHMS
Gaussian Processes for Dummies (blog post)
A Tutorial on Bayesian Optimization for Machine Learning (slides)
Introduction to Bayesian Optimization (slides)
Tutorial: Gaussian process models for machine learning (slides)

The prior distribution in Bayesian optimization is called a Gaussian process on the prior. This terminology was confusing to me at first since I thought that Bayesian optimization was basically synonymous with Gaussian processes, but I think the prior distribution is called a Gaussian process. Gaussian processes are used as a machine learning method.

What exactly the posterior and the prior are doing was confusing to me as well as some people in the class. At first I thought that the prior was a distribution on functions. For example, if you had a polynomial function with parameterized coefficients, theta, then I thought that the prior and the posterior were a distribution on these coefficients theta, but this is not correct. Thus, initially, I thought that the prior must specify a family of functions.

The prior distribution and the posterior distribution are distributions on function values without regard to the type or family of function. Hence, each possible function value for a given input has a probability assigned by the distribution. A common choice for a prior distribution on the function values is a normal distribution centered at 0 with some variance. This means that the function that maximizes the probability of this distribution is y = 0. The posterior distribution gives a probability distribution on possible function values after function evaluations are performed and incorporated with the likelikhood function, which is jointly normal on the observed function evaluations.

There is an animated GIF in some slides on page 28 that I found that gives a nice visualization of this phenomena: Introduction to Bayesian Optimization (slides).

Since the normal prior centered at 0 is usually chosen, I wonder how much the choice of prior changes things. The prior in a machine learning context could be the average results that given hyperparameters produce across many machine learning projects. There are statistics to calculate the relative effects of the prior and the likelihood on the posterior distribution. It is often the case that the prior has little effect while the likelihood has a greater effect especially with more data; thus, optimizing the prior distribution could be a lot of effort for little gain.

The Meaning and Selection of the Kernel

In Bayesian optimization, there is a function to determine the covariance between any two function evaluation points. This function determines the covariance matrix used in the multivariate Gaussian matrix for the likelihood function. The covariance function is called a kernel, and there are many kernels used in Gaussian processes.

The paper that we discussed in class, Practical Bayesian Optimization of Machine Learning Algorithms, discussed two kernels, the squared exponential kernel and the Matérn 5/2 kernel. The authors argue that the squared exponential kernel is too smooth for hyperparameter tuning in machine learning while the Matérn kernel is more appropriate. The papers show the Matérn kernel performing better in some empirical experiments.

How was this kernel really chosen? Did the authors simply try several kernels in their experiments and found one that performed the best? This doesn’t really give a provable way to choose a good kernel. We wondered whether there was some mathematically formal way to prove that some kernel was better than another, but we thought that this was probably not the case. Maybe it could be proven given certain conditions such as convexity or smoothness assumptions. Intuitively, similar choices of hyperparameters will probably produce similar results, so kernels that assume a somewhat smooth function are probably appropriate.

One of the drawbacks of Bayesian optimization in machine learning hyperparameter tuning is that Bayesian optimization has its own hyperparameters that could be tuned, so this just pushes back the problem of hyperparameter tuning. How are the hyperparameters of Bayesian optimization meant to be tuned? The choice of kernel, acquisition function, prior distribution, and stopping criteria are examples of hyperparameters for Bayesian optimization.

The Meaning of the Acquisition Function

In Bayesian optimization, an acquisition function is used to choose the next point for function evaluation. The paper that we discussed in class mentions three acquisition functions: probability of improvement, expected improvement, and upper confidence bound.

The definition of these functions is very abstract and mathematical, and I had some difficulty interpreting what the functions did. This makes reasoning about them intuitively difficult. The paper focuses on the expected improvement function, and I found an alternative formula for it on slide 35 of the presentation Introduction to Bayesian Optimization. This formula is the following.

∫ max(0, y_{best} – y) p(y | x; \theta, D) dy

From this formula, it is clearer that the expected improvement formula finds a point that maximizes the probability that the function evaluation at that point will be below the best y value found so far. Perhaps the other formulas can be written in a similar manner, giving a better understanding of what they do.

The paper did not present a mathematically formal way of choosing the best acquisition function. Maybe under certain conditions, a given acquisition function can be shown to be optimal.

Saddle-Points in Non-Convex Optimization

Identifying the Saddle Point Problem in High-dimensional Non-convex Optimization (Mukund)

Non-Convex Optimization

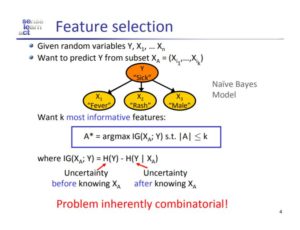
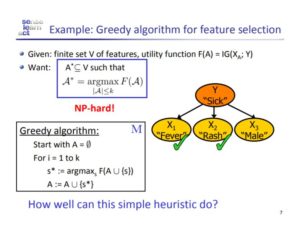
Non-convex optimization problems are any group of problems which are not convex (concave, linear etc.). These non-convex optimization problems are difficult to solve because non-convex functions have potentially many local minima and finding the global minima among all the local minima is hard. For this reason, solving such optimization problems are at least NP-Hard. Other reasons which make optimizing non-convex problems are

the presence of saddle points
very flat regions exhibited in the curvature
the curvature of such functions can be widely varying.

Traditionally, methods like Gradient descent, Newton Methods which are used to solve convex optimization problems are used to solve non-convex optimization problems as well.

Saddle Points

Given a function f, a critical point is defined as the point in the function where the derivative of f becomes 0. Typically, critical points are either maxima or minima (local or global) of that function. Saddle points are special type of critical points where the slope becomes 0, but are not local extremum in both axes.

For example, in the graph ${z = x^2 - y^2}$ , the point (0,0) is the saddle point because the gradient at (0,0) is 0, but the point in neither a local maxima not a local minima.

At this point, let us talk a bit more about critical points. The curvature of the function surrounding these critical points can tell us a lot about these critical points itself. The curvature of the function can be evaluated using the Hessian at these points. The eigen values of the Hessian at the critical point can describe the critical point.

If the eigen values are all non-zero and all positive, then the critical point is local maxima
If the eigen values are all non-zero and all negative, then the critical point is local minima
If the eigen values are all non-zero and mix of both positive and negative values, then the critical point is saddle point
If the Hessian matrix is singular, then the critical point is a degenerate critical point

Saddle Point Problem in High Dimensional Non-convex Problems

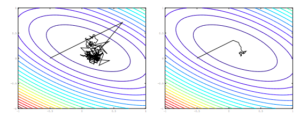
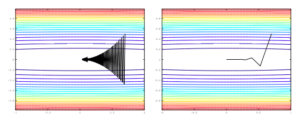
When a non-convex error function has a single scalar variable, there might be a lot of local maxima and local minima in the function but there is very negligible probability of occurrence of a saddle point. Whereas error functions with N scalar variables are likely to have more saddle points than local minima. In fact, as the dimensionality (N) increases, the number of saddle points increases exponentially. There have been many studies to prove this point. When dealing with high dimensional non-convex problems, which is the case with real world problems, we have to deal with these saddle points. The traditional methods like gradient descent and Newton methods perform poorly in presence of these saddle points. The gradient descent methods are repelled away from these saddle points, but the convergence is painfully slow. Whereas the Newton methods in an effort to speed up convergence, get attracted to these saddle points and do not converge on the local minima.

Dynamics of Optimization Algorithms around Saddle Points

To better understand the difficulty of existing optimization algorithms for high dimensional non-convex problems, it is helpful to understand how these algorithms behave near saddle points during the optimization process.

We can re-parameterize the critical points using the Taylor expansion so that they can be locally analysed. The Taylor expansion can be given as:

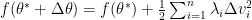
$f(\theta^* + \Delta \theta) = f(\theta^*) + \frac {1}{2} \sum_{i=1}^{n} \lambda_{i} \Delta v_{i}^2$

The step size that the gradient descent method uses is $-2 \lambda_i \Delta v_i$ . A step of the gradient descent method will always move in the right direction around the saddle point. If the eigen value is positive, we move towards that point in the direction of the negative curvature and hence the gradient descent method will always move away from the saddle points. The problem with gradient descent is the step size. Because gradients are proportional to corresponding eigenvalues, eigenvalues dictates how fast we move in each direction. If there is a large discrepancy in eigenvalues, the gradient descent will take very small steps.†It might take a very long time to move away form the critical point, if the critical point is a saddle point, or to the critical point if it is a minimum.

The Newton method rescales the gradients in each direction with the inverse of the corresponding eigenvalue. The step size used in the Newton method is 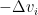$- \Delta v_{i}$ . If the eigenvalue is negative, the Newton method moves in the opposite direction to the gradient descent method due to the rescaling. This results in moving in the wrong direction around the saddle points and Newton methods instead of escaping the saddle point converge on them.

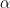The trust region is a second order method, where the step size taken is $- ( \frac {\lambda_i} {\lambda_i + \alpha} ) \Delta v_i$ . This speeds up the convergence significantly and this method moves in the same direction as the gradient descent method, thus escaping the saddle points. It can also suffer the drawback of slow convergence sometimes if $\alpha$ is too large.

Attacking the Saddle Point Problem in High-dimensional Non-convex Optimization (Yufeng)

Problems with Stochastic Gradient Descent (SGD) and Newton Method

Based on our previous analysis, we know that saddle points are ubiquitous in high dimensional non-convex optimization problems. However, we are still uncertain about how modern optimizers would behave around these saddle points. Specifically, we would like to focus on Stochastic Gradient Descent (SGD) and Newton method here.

Suppose we have a function 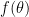$f(\theta)$ , in which 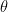$\theta$ stands for the whole parameters of a model that we want to optimize. Besides, we have a saddle point 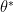$\theta^*$ . Then we may approximate 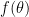$f(\theta)$ around this saddle point using second-order Taylor expansion by

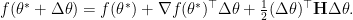
$f(\theta^* + \Delta\theta) = f(\theta^*) + \nabla f(\theta^*)^\top \Delta\theta + \frac{1}{2} (\Delta\theta)^\top \mathbf{H} \Delta\theta.$

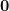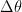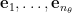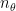Since a saddle point is also a critical point, the second first-order term can be cancelled with $\nabla f(\theta^*)$ being a $\mathbf{0}$ vector. Now let’s reparametrize $\Delta\theta$ based on how it changes along orthonormal eigenvector directions of the Hessian matrix $\mathbf{H}$ , i.e., $\mathbf{e}_1, \dots, \mathbf{e}_{n_\theta}$ . Here $n_{\theta}$ represents the number of eigenvectors for $\mathbf{H}$ . 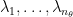Correspondingly, we also have eigenvalues $\lambda_1, \dots, \lambda_{n_\theta}$ . Then the movement along eigendirections can be formulated as

$\begin{aligned} \Delta \mathbf{v} &= \left[ \begin{array}{c} e_1^\top\\ \vdots\\ e_{n_\theta}^\top \end{array} \right] \Delta\theta \end{aligned}.$

Since a Hessian matrix should be both real and symmetric, with orthonormal eigenvectors, it can be represented by

$\mathbf{H} = [ e_1, \dots, e_{n_\theta} ] \Lambda \left[ \begin{array}{c} e_1^\top \\ \vdots \\ e_{n_\theta}^\top \end{array} \right],$

where $\mathbf{\Lambda}$ is the matrix with eigenvalues on the diagonal. Therefore, our Taylor expansion approximation can be expressed as:

$\begin{aligned} f( \theta^* + \Delta\theta ) &= f(\theta^*) + \frac{1}{2} (\Delta\theta)^\top \overbrace{ [ e_1, \dots, e_{n_\theta} ] \mathbf{\Lambda} \left[ \begin{array}{c} e_1^\top \\ \vdots \\ e_{n_\theta}^\top \end{array} \right] }^{\mbox{ Orthonormal }} \Delta\theta \\ &= f(\theta^*) + \sum_{i=1}^{n_\theta} \lambda_i \Delta\mathbf{v}_i^2 \end{aligned}.$

Based on the above reparametrization, we can now go forward with how SGD and Newton method stroll around the saddle point 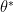$\theta^*$ . First for SGD, the movement along a specific eigenvector 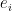$e_i$ is defined as

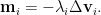
$\mathbf{m}_i = -\lambda_i \Delta\mathbf{v}_i.$

It’s worth mentioning that we are actually moving along the correct direction here. However, with $\lambda_i$ scaling before $\Delta\mathbf{v}_i$ , eigenvalues of different magnitudes will result in different step sizes along eigenvector directions.

While for Newton method, the movement is quantified by

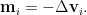
$\mathbf{m}_i = - \Delta\mathbf{v}_i.$

Although the magnitude of movement is forced to be the same by rescaling with the eigenvalues, negative eigenvalues can actually cause the resulting shift going in the opposite direction. This will unexpectedly increase the loss. Furthermore, since Newton method is originally developed to find roots of an equation, as it applied here on the first derivatives of the original objective function, it can eventually help to find all the critical points iteratively.

General Trust Region Methods

In order to tackle the saddle point problem, the authors defined a class of generalized trust region methods (GTRM), which is the extension of classical trust region method (CTRM). First of all, let’s look at how CTRM works. We’ll use second-order Taylor expansion (quadratic model) to approximate the original objective function

$\begin{aligned} \Delta\theta &= \text{argmin}_{\Delta\theta} f(\theta) + \nabla f(\theta)^\top \Delta\theta + \frac{1}{2} \Delta\theta^\top \mathbf{H} \Delta\theta \\ & \mbox{s.t. } ||\Delta\theta|| \le \Delta, \end{aligned}$

in which 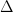$\Delta$ defines the radius of a trust region. While for their proposed GTRM, they made two changes:

The minimization of first-order Taylor expansion is allowed, which can in some way alleviate the difficulty of optimization;
Original norm constraints on the step 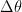$\Delta\theta$ are relaxed, which is replaced by some hand-designed distance metrics.

With these extensions, the generalized trust region methods can be summarized as:

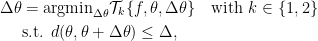
$\begin{aligned} \Delta\theta &= \text{argmin}_{\Delta\theta} \mathcal{T}_k\{ f, \theta, \Delta\theta \} \quad \mbox{with }k \in \{1,2\} \\ & \mbox{s.t. } d( \theta, \theta + \Delta\theta ) \le \Delta, \end{aligned}$

in which 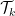$\mathcal{T}_k$ represents the 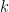$k$ -th order Taylor expansion and $d( \theta, \theta + \Delta\theta )$ defines some distance metrics.

Attacking the Saddle Point Problem

Now let’s get back to how we should attack the saddle point challenge that can’t be completely solved by either SGD or Newton method. It would be straightforward to consider combining the advantages of both methods. Intuitively, we can just rescale the SGD movement by the absolute value of corresponding eigenvalues, i.e.,

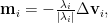
$\mathbf{m}_i = - \frac{\lambda_i}{|\lambda_i|} \Delta \mathbf{v}_i,$

which uses the same rescaling as the Newton method but owns the property of moving in the correct eigendirection. However, there hasn’t been any mathematical justification of such designs before. Then we’ll need to answer two potential questions:

Are we optimizing the same objective function, if we replace $\mathbf{H}$ with $|\mathbf{H}|$ which is the matrix obtained by taking the absolute value of each eigenvalue of $\mathbf{H}$ ?
The above expectation might be true near the saddle points (or more generally the critical points), will it still work well when it’s far away from the critical points?

With the above concerns, the authors were able to show that this is actually a valid heuristic design based on their GTRM framework.

To begin with, a first-order Taylor expansion of the objective function is used as the main goal for optimization as:

$\Delta\theta = \text{argmin}_{\Delta\theta} \mathcal{T}_1\{ f, \theta, \Delta\theta \} = f(\theta) + \nabla f(\theta)^\top \Delta\theta,$

which is just an affine transformation so that the minimum will always be negative infinity if there are no constraints on the input domain. Accordingly, we know the minimizer should lie on the boundary of the trust regions. Besides, we need to incorporate the curvature information into this optimization problem, which will have to come from inside the distance metric in constraints. Here in this paper, the authors restrict the trust region to be defined by how far the second-order Taylor expansion can be away from the first-order expansion. Formally, the distance constraint is defined as

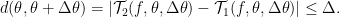
$d( \theta, \theta + \Delta\theta ) = |\mathcal{T}_2(f,\theta, \Delta\theta) - \mathcal{T}_1(f,\theta, \Delta\theta) | \le \Delta.$

If expand the distance constraint, we can get

$\frac{1}{2} \left| \Delta\theta^\top \mathbf{ H }\Delta\theta \right| \le \Delta .$

This quadratic problem will not be that easy to solve if 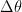$\Delta\theta$ is of high dimension. To circumvent this, the authors proposed a Lemma as shown below.

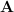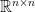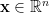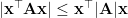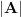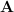Lemma 1. Let $\mathbf{A}$ be a nonsingular symmetric matrix in $\mathbb{R}^{n\times n}$ , and $\mathbf{x}\in \mathbb{R}^n$ be any vector. Then it holds that $\mathbf{|x^\top Ax | \le x^\top |A|x}$ , where $|\mathbf{A}|$ is the matrix obtained by taking the absolute value of each of the eigenvalues of $\mathbf{A}$ .

Proof. 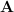$\mathbf{A}$ is nonsingular and symmetric $\Rightarrow$ $\{e_1, e_2, \dots, e_n\}$ are orthogonal. If they have been normalized, then $\mathbf{I} = \sum_i e_ie_i^\top$ .

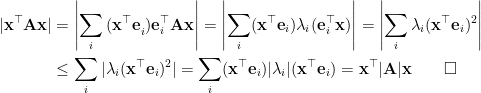
$\begin{aligned} |\mathbf{x^\top Ax} | &= \left| \sum_i \mathbf{ (x^\top e}_i ) \mathbf{e}_i^\top \mathbf{A x }\right| = \left| \sum_i (\mathbf{x^\top e}_i )\lambda_i (\mathbf{e}_i^\top \mathbf{x}) \right| = \left| \sum_i \lambda_i (\mathbf{x}^\top \mathbf{e}_i)^2 \right| \\ & \le \sum_i |\lambda_i (\mathbf{x}^\top \mathbf{e}_i)^2| = \sum_i (\mathbf{x}^\top \mathbf{e}_i) | \lambda_i | (\mathbf{x}^\top \mathbf{e}_i) = \mathbf{ x^\top |A| x } \quad\quad \square \end{aligned}$

Therefore, instead of using the original constraint formula, we can fold 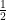$\frac{1}{2}$ into the right-hand side distance upperbound and relax it a little bit as

$\left| \Delta\theta^\top \mathbf{ H }\Delta\theta \right| \le \Delta\theta^\top |\mathbf{ H }|\Delta\theta \le \Delta.$

As we have already stated that such minimizer will always lie on the boundary of the trust region, we can further remove the inequality sign. Our final optimization problem becomes

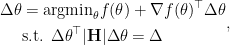
$\begin{aligned} \Delta\theta &= \text{argmin}_{\theta} f(\theta) + \nabla f(\theta)^\top \Delta\theta \\ & \mbox{s.t. } \Delta\theta^\top |\mathbf{H}| \Delta\theta = \Delta \end{aligned},$

which can be solved analytically by Lagrangian multiplier method.

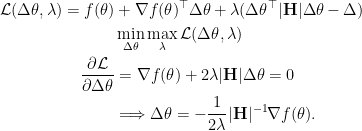
$\begin{aligned} \mathcal{L}( \Delta\theta, \lambda ) = f(\theta) &+ \nabla f(\theta)^\top \Delta\theta + \lambda ( \Delta\theta^\top |\mathbf{H}| \Delta\theta - \Delta ) \\ &\min_{\Delta\theta} \max_{\lambda} \mathcal{L}( \Delta\theta, \lambda ) \\ \frac{\partial \mathcal{L}}{\partial \Delta\theta } &= \nabla f(\theta) + 2\lambda |\mathbf{H}| \Delta\theta = 0\\ & \Longrightarrow \Delta\theta = -\frac{1}{2\lambda} |\mathbf{H}|^{-1} \nabla f(\theta). \end{aligned}$

If the scalar in front is folded into learning rate, an update step would be

$\Delta\theta = -|\mathbf{H}|^{-1} \nabla f(\theta).$

This is called saddle-free Newton method (SFN), which inherits the merits of both SGD and Newton method.

It can move further (less) in the directions of low (high) curvature as compared to SGD.
With always correct directions, it can move away from saddle points when the Hessian matrix is not positive definite.

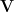However, the exact computation of a Hessian matrix would be infeasible in a high dimensional problem. To escape from exact computation, the authors introduce the Krylov subspace method, which tries to optimize upon another space that is much lower than the original space, i.e., $\hat{f}(\alpha) = f(\theta + \alpha \mathbf{V} )$ . Here $\mathbf{V}$ stands for the 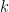$k$ largest eigenvectors of the Hessian matrix. Such eigenvectors can be found efficiently through Lanczos iteration as stated in their paper. So it should be noted that now we are optimizing on the variable $\alpha$ . Afterward, the new absolute value version Hessian matrix associated with this new space is calculated via eigendecomposition for $|\hat{\mathbf{H}}| \leftarrow \left| \frac{\partial^2 f}{\partial \alpha^2} \right|$ . Thereafter, Newton method similar steps can be applied iteratively. The authors also involve another step to determine the learning rate (step size) for their SFN method. The overall pseudocode is shown in Algorithm 1 in the following figure.

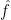As we mentioned before, line 8 above is applied to search for a suitable learning rate $\lambda$ that can minimize current $\hat{f}$ from our understanding. Then in line 9, it’s mapped back to the original parameter space ( 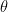$\theta$ ) and the final update is done eventually.

Experimental Validation

After theoretical analysis above, it’s essential to validate these results experimentally. In this section, the existence of saddle points, the effectiveness of SFN on the deep feed-forward neural network and recurrent neural network are elaborated through various experiments.

The Existence of Saddle Points in Neural Networks

In order to compare with other popular optimizers like SGD and damped Newton method exactly, small neural networks on downsampled MNIST and CIFAR-10 are trained, which enables exact computation of updates. The experimental results are shown in the following figure.

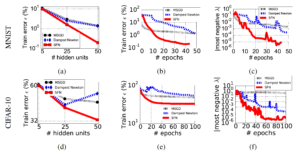
Based on the above figure, we can observe that:

In (a) and (d), as the number of hidden units increases, our model become much more high-dimensional. It’s obvious that both SGD and damped Newton method get stuck around a hidden unit number of 25. However, for their proposed SFN, it’s still able to step into a region of much lower error. This indirectly indicates that the number of saddle points increases exponentially as the dimensionality of model increases.
From (b) and (e) of learning curves plotted in terms of epochs, it confirms that SFN can evade away from saddle points and achieves a much lower training error. While for SGD and damped Newton method, both get trapped in regions where SFN does not.
Finally, from (c) and (f), the evolution of the absolute value of most negative eigenvalue is shown, which shows that it moves more toward the right as we achieve a lower error. So we are gradually having a more positive definite Hessian matrix. This indicates a local minimum instead of saddle points, for which we have successfully escaped.

The Effectiveness of Saddle-Free Newton Method

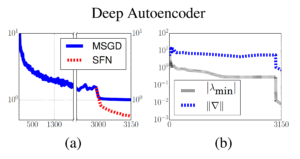
Furthermore, the authors tried to verify that their SFN method is also able to repel away from saddle points and achieves local minimum under deep neural networks. A seven-layer deep autoencoder is trained on the full-scale MNIST dataset, the approximate SFN jumps in after mini-batch SGD got stuck. The learning curve is shown in (a) of the figure below. We can also discover that after SFN is incorporated, the magnitude of the absolute value of the minimum eigenvalue and the norm of gradients have been reduced significantly.

Recurrent Neural Network Optimization

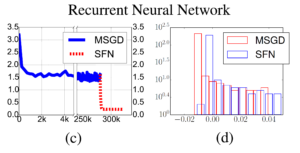
In the end, the authors tried to test if SFN is able to help training the recurrent neural network (RNN) if the training difficulty is caused by saddle points. A small RNN with $120$ hidden units targeted for character-level language modeling is trained on the classical Penn Treebank dataset. Again SFN was used after SGD got trapped. A similar trend for learning curve is found as shown in (c) of the following figure. Furthermore, we can see in fig (d) that the Hessian matrix of the final solution found by SFN has much fewer negative eigenvalues as compared to ones found by mini-batch SGD.

Alternating Direction Method of Multipliers (ADMM)

1. Introduction

This blog post covers analysis of Alternating Direction Method of Multipliers (ADMM); which solves Convex Optimization problems by breaking the problems into subproblems efficiently. Sections: ${1}$ to ${6}$ are written by Nischel Kandru and rest of them by Ahmadreza Azizi.

2. Dual Ascent

${\rightarrow}$ Consider the Convex Optimization problem which minimizes ${f(x)}$ such that ${Ax = b}$ .

Lagrangian for this problem is:
${L(x,y) = f(x) + y^T (Ax-b)}$

Dual problem of the original problem is:
${g(y)= max_{y} -f^{*}(-A^{T}y) -b^{T}y}$ , where ${f^*}$ is the convex conjugate of the objective function ${f}$ and ${y}$ is the dual variable or the lagrange multiplier.

${\rightarrow}$ If strong duality holds, then the optimal values of the primal and dual problems are the same.

${x^* = argmin_x \quad L(x,y^*)}$

where ${x^*}$ is the primal optimal point and ${y^*}$ is the dual optimal point; provided there is only one minimizer of ${L(x,y^*)}$ ( ${f}$ is strictly convex)

${\rightarrow}$ If ${f}$ is just convex (implies there isn’t a unique minimizer), instead dual-subgradient is performed rather than dual gradient;

${x^* \in argmin_x \quad L(x, y^*)}$

${\rightarrow}$ In the dual ascent method, to solve the dual problem, gradient ascent method would be used. Assuming ${g}$ is differentiable, we find:
${x^+ = argmin_x L(x,y)}$ and ${\nabla g(y) = Ax^+ - b}$

${\rightarrow}$ If ${g}$ is non-differentiable, we use sub-gradient method to solve the minimization problem:

${x^{k+1} = argmin_x L(x,y^k)}$ : x-minimization step
${y^{k+1} = y^k + \alpha^k (Ax^{k+1} - b)}$ : dual variable update,
where ${k}$ is the iteration step and ${\alpha^k}$ is the step sizes.

Repeat the above steps iteratively to solve the optimization problem. This is called dual ascent; because with appropriate step size ${\alpha^k}$ , we always get ${g(y^{k+1}) > g(y^k)}$ .

Let’s derive the above minimization steps:

Given ${f}$ , an objective function then the conjugate of the function: ${f^*(y) = max_{x \in R^n} \quad y^T x - f(x)}$ ; maximum over all points ${x}$ evaluated at point ${y}$ .

If ${f}$ is closed and convex, then ${f^{**} = f}$ ; conjugate of conjugate is the function itself. Also, ${x \in \partial f^* (y)}$ if and only if ${y \in \partial f(x)}$ if and only if ${x \in argmin_x f(x) - y^Tx}$ ; if ${x}$ is the subgradient of the conjugate at ${y}$ , if and only if ${y}$ is the subgradient of the original function at ${x}$ .

${x \in \partial f^*(y)}$ if and only if ${x \in argmin_x f(x) -y^Tx}$ , sub-gradient for maximum is the one that achieves the maximum. We also know that achieving maximum is same as achieving minimum; so
${x \in argmin_x -(y^Tx - f(x))}$
${\implies x \in argmin_x (f(x) - y^Tx)}$

Dual problem:
${g(y) = max_y -f^*(-A^Ty) - b^Ty}$ — (1)
Suppose ${G(y) = f^*(-A^Ty)}$
Subgradients of (1) are: ${\partial G(y) - b}$ where;
${\partial G(y) = A \partial f^* (-A^Ty)}$
${x \in \partial F^* (-A^Ty)}$ if and only if ${x \in argmin_x f(x) + y^TAx}$

${x^{k+1} \in argmin_x f(x) + {y^k}^TAx}$
${\implies x^{k+1} \in L(x,y^k)}$
${y^{k+1} = y^k + \alpha^k (Ax^{k+1} -b)}$

Disadvantages of Dual Ascent

Slow Convergence
Even though we may achieve convergence in dual objective value, convergence of ${y^k}$ , ${x^k}$ to solutions require strong assumptions

Advantages of Dual Ascent
Decomposability; which leads to Dual Decomposition

3. Dual Decomposition

If ${f}$ is separable, then dual ascent can be decentralized.

${f(x) = \sum_{i=1}^{N} f_i (x_i)}$

The Lagrangian for this problem would be:

$\displaystyle L(x,y) = \sum_{i=1}^{N} L_i (x_i, y) = \sum_{i=1}^{N} (f_i (x_i) + y^TA_ix_i - (1/N)y^Tb)$

$\displaystyle {x_i}^{k+1} := argmin_{x_i} L_i(x_i, y^k)$

we can compute the x-minimization steps in parallel, thanks to the decomposability.

$\displaystyle y^{k+1} := y^k +\alpha^{k} (Ax^{k+1} -b)$

This essentially involves couple of steps:

Broadcast: Send ${y}$ to each of the other nodes, each optimizes in parallel to find ${x_i}$
Gather: Collect ${A_ix_i}$ from each node, update the global dual variable ${y}$

4. Augmented Lagrangian and Method of Multipliers

To yield convergence without assumptions like strict convexity, we add a new term; so that the function becomes more convex.

$\displaystyle L_{\rho} (x,y) = f(x) + y^T(Ax-b) + \frac{\rho}{2}{||Ax-b||_2}^2$

where ${\rho > 0}$ is the penalty parameter

We can clearly see that the addition of the new term doesn’t change the problem as such, because the constraint is ${Ax=b}$ . The new term provides:

Numerical Stability
Smooths out the primal criterion function
Introduces curvature into the objective function

Augmented Lagrangian can be viewed as the Lagrangian with problem-

$\displaystyle min \quad f(x) + \frac{\rho}{2}{||Ax-b||_2}^2$

subject to ${Ax = b}$

${\rightarrow}$ With the penalty term ${\rho}$ , dual function ${g_\rho}$ can be shown to be differentiable under rather mild conditions on the original problem.

${\rightarrow}$ Applying dual ascent yields:

${x^{k+1} := argmin_x L_\rho (x,y^k)}$
${y^{k+1} := y^k + \rho (Ax^{k+1} -b)}$

${\rightarrow}$ Optimality conditions for original problem are primal and dual feasibility, i.e,

$\displaystyle Ax^* - b = 0, \nabla f(x^*) + A^Ty^* = 0$

Let’s see the motivation behind having ${\rho}$ as the stepsize instead of ${\alpha^k}$ .

${\nabla L_\rho {(x, y^k)}_{x=x^{k+1}} = 0}$ , since ${x^{k+1}}$ minimizes
${\nabla f(x^{k+1}) + A^Ty^k + \rho A^T (Ax^{k+1} - b) = 0}$
${\nabla f(x^{k+1}) + A^T(y^k + \rho(Ax^{k+1} - b)) = 0}$
${\nabla f(x^{k+1}) + A^T(y^{k+1}) = 0}$
${(x^{k+1}, y^{k+1})}$ is dual feasible

${\rightarrow}$ This is the stationary condition for original problem, so to preserve this use ${\rho}$ as stepsize.
${\rightarrow}$ We get much better convergence in Augmented Lagrangian, but lose out on the decomposability; the solution to this is ADMM which gets the best out of both the worlds.

5. Alternating Direction Method of Multipliers

ADMM combines Decomposability of Dual Ascent and the convergence of Method of Multipliers.

$\displaystyle min \quad f(x) + g(z)$

where ${f}$ and ${g}$ are convex, subject to ${Ax+Bz=c}$

The Lagrangian for this problem is:
${L_\rho (x,z,y) = f(x) + g(z) + y^T(Ax+Bz-c) + \frac{\rho}{2}{||Ax+Bz-c||_2}^2}$

${x^{k+1} := argmin_x L_\rho (x, z^k, y^k)}$ — X- minimization step
${z^{k+1} := argmin_z L_\rho (x^{k+1}, z, y^k)}$ — Z- minimization step
${y^{k+1} := y^k + \rho (Ax^{k+1} + Bz^{k+1} -c)}$ — dual variable update step

${\rightarrow}$ ${x}$ and ${z}$ are updated in an alternating fashion.
${\rightarrow}$ We can clearly see that the Z- minimization step depends on the updated value ${x^{k+1}}$ ; so these steps cant be parallelized completely.

The method of multipliers for this problem would have the form:

$\displaystyle (x^{k+1}, z^{k+1}) := argmin_{x,z} L_\rho (x,z,y^k)$

$\displaystyle y^{k+1} := y^k + \rho (Ax^{k+1} +Bz^{k+1} -c)$

we can clearly see that, here we try to minimize ${x}$ and ${z}$ together and lose out on the decomposability.

${\rightarrow}$ We force decomposability in ADMM, we dont have complete power of decomposability as ${z^{k+1}}$ depends on ${x^{k+1}}$ but we can compute all the ${x_i}$ s and ${z_i}$ s parallely.

${\rightarrow}$ We can see that ADMM doesnt converge as much as the Method of Multipliers and doesnt decompose as much as Dual Decomposition. But, it takes the best of both worlds.

${\rightarrow}$ ADMM in general requires lot of iterations for highly accurate solutions, but obtains relatively accurate solution in few iterations.

Scaled Form
We can have a scaled dual variable as: ${u= \frac{1}{\rho}y}$ and this makes the computations efficient.

$\displaystyle x^{k+1} := argmin_x (f(x) + \frac{\rho}{2}{||Ax+Bz^k-c+u^k||_2}^2)$

$\displaystyle z^{k+1} := argmin_z (g(z) + \frac{\rho}{2}{||Ax^{k+1}+Bz-c+u^k||_2}^2)$

$\displaystyle u^{k+1} := u^k + Ax^{k+1} +Bz^{k+1} -c$

6. References

http://stanford.edu/~boyd/admm.html
http://www.stat.cmu.edu/~ryantibs/convexopt-F13/lectures/23-dual-meth.pdf

Convex Optimization with Submodular Functions

During our introductory lecture on submodular functions, based on Francis Bach’s paper, we discussed the importance of combinatorial optimization for machine learning applications, reviewed set notation, and defined the key concepts from chapters 2-3 of Bach’s paper.

Importance of Combinatorial Optimization for Machine Learning

Feature selection, factoring distributions, ranking, clustering, and graph cuts were given as examples of machine learning problems that are combinatorial by nature and require either maximization or minimization. When discussing the importance of submodular functions and combinatorial optimization, we referred to the feature selection example from this slide deck produced by professors Andreas Krause and Carlos Guestrin.

In the feature selection example, we desire to choose the k best features that will add the most certainty in predicting the dependent variable (in this example, Y = “Sick”). As Krause and Guestrin point out, this problem is inherently combinatorial and therefore requires combinatorial optimization techniques. The goal of choosing an optimal feature set, |A*| ≤ k, is outlined in the first two slides. The problem is NP-hard because there are (2^p) – 1 constraints so we use a greedy algorithm to solve it. This essentially means that we take the best individual element that minimizes the marginal uncertainty of adding it to the current optimal set, A*. We repeat this process for up to k iterations until our optimal set is finalized. Although this certainly isn’t going to give us the true optimal set every time because some combinations of features may be more optimal when paired together, Krause and Guestrin inform us that it does give us a guarantee of at least 1 – 1/e (~63%) sub-optimal performance.

Background

Before covering the Bach paper material, we reviewed set function notations for those people who hadn’t taken a discrete math or combinatorics class. The slide below outlines the notations covered during our class lecture.

The three notations at the bottom of the slide seemed to be the ones that students were least familiar with. Cardinality (absolute value signs around a set) is simply the number of elements contained within a given set. The indicator vector, 1_A, for the set A is simply a vector with a 1 in a particular dimension if the element corresponding to that vector dimension is contained in the set A and is a 0 if it isn’t. Lastly, the notation V \ A is simply set V with subset A removed.

Submodular Functions and the Lovász Extension

When we introduced submodular function notation, we used both Definition 2.1 and Proposition 2.2 from the book. When first learning about submodularity, we found that the proposition 2.2, which introduces the property of diminishing returns, was more intuitive and made understanding definition 2.1 easier.

To further ring home the concept of submodular functions and the property of diminishing returns, we reviewed the set cover example from the Krause and Guestrin slides below. The goal of this visual aid was to demonstrate how adding a new element to a set A, a subset of set B, can only cover the same or more surface area than adding the same new element to set B.

During the next part of the lecture, we reviewed associate polyhedra which was by far the most confusing material to cover for the class. The differences between submodular and base polyhedra expressed in Bach’s paper is clear to understand. The base polyhedra, B(F), can be thought of as the hollow outer shell of the set function formed by the intersecting constraint hyperplanes and the submodular polyhedra, P(F), can be thought of as the base polyhdra and the discrete, encapsulated, non-empty interior space encompassed by the base polyhedra. What we found confusing was whether Figure 2.1 below was representing just the domain of the set function, F, or if it was also representing the function values. We agreed that we thought the figure was only representing the domain, because it would need an additional dimension to represent the set function values for the elements s1, s2, and s3.

Finally, we had the opportunity to introduce the Lovász extension (also referred to as the Choquet integral) which allows us to extend the vertices of a {0,1}^p hypercube to a continuous [0, 1]^p hypercube (think of taking the convex hull of the vertices). By dividing the continuous hypercube into p! simplices, we can create areas with ordered variable values like in the figures from Bach’s paper below.

One of the last things we were able to cover in class was the properties of the Lovász extension. The Lovász extension is important mainly because it allows us to create a continuous extension of discrete problems. Additionally, it has a unique connection with submodularity and convexity. A set function is submodular if and only if its Lovász extension is convex. We ended the class by proving this theorem.

Theorem: A set-function, F, is submodular if and only if its Lovász extension, f, is convex. 

Proof: Let's assume f is convex. Let A, B ⊆ V. The vector,

has components equal to 0 where [ V \ (A ∪ B) ]
                        2 where [ A ∩ B ] 
                    and 1 where [ A Δ B = (A \ B) ∪ (B \ A) ].

Using the property,

we get

Since f is convex, then

Therefore, F(A) + F(B) = F(A ∪ B) + F(A ∩ B). This satisfies the definition of convexity, therefore if F is submodular, then it is sufficient that for all ω ϵ ℝ^p, f(ω) is a maximum of linear functions, thus it is convex on ℝ^p.

Adam

This post presents a summary of the background and class discussion on the Adam (adaptive moment estimation) algorithm. The primary source for this discussion was the original Adam paper. Adam is quite possibly the most popular optimization algorithm being used today in machine learning, particularly in deep learning.

Background (Ryan Kingery)

Adam can be thought of as a generalization of stochastic gradient descent (SGD). It essentially combines three popular additions to SGD into one algorithm: AdaGrad, Nesterov momentum, and RMSProp.

Adam = AdaGrad + momentum + RMSProp

Recall from a previous post that AdaGrad modifies SGD by allowing for variable learning rates that can hopefully take advantage of the curvature of the objective function to allow for faster convergence. With Adam we extend this idea by using moving averages of the gradient moment estimates to smooth the stochastic descent trajectory. The idea is that smoothing this trajectory should speed up convergence by making Adam converge more like batch gradient descent, but without the need of using the entire dataset.

To discuss momentum and RMSProp we must recall the definition of an exponentially weighted moving average (EWMA), also called exponential smoothing or infinite impulse response filtering. Suppose we have a random sample $x_1,\cdots,x_T$ of time-ordered data. An EWMA generates a new sequence $m_1,\cdots,m_T$ defined by

$m_t = \beta m_{t-1} + (1-\beta)x_t = (1-\beta) \sum_{i=1}^t \beta^{t-i}x_i.$

The hyperparameter $0 \leq \beta \leq 1$ is called a smoothing parameter. Intuitively, the EWMA is a way of smoothing time-ordered data. When $\beta \approx 0$ , the EWMA sequence depends only on the current value of $x_t$ , which just gives the original non-smoothed sequence back. When $\beta \approx 1$ , the EWMA doesn’t depend at all on the current value $x_t$ , which results in a constant value for all $m_t$ .

The EWMA is useful when we’re given noisy data and would like to filter out some of the noise to allow for better estimation of the underlying process. We thus in practice tend to favor higher values of $\beta$ , usually 0.9 or higher. It is precisely this idea that momentum and RMSProp exploit. Before mentioning this, though, a minor point.

It turns out that the EWMA tends to produce bias estimates for the early values $x_t$ . When the process hasn’t generated enough data yet, EWMA sets all the remaining values it needs to 0, which tends to bias the earlier part of the EWMA sequence towards 0. To fix this problem, one can use instead a bias-corrected EWMA defined by

$\hat m_t = \frac{m_t}{1-\beta^t}.$

One might naturally ask whether this bias correction term is something to worry about in practice, and the answer, of course, is it depends. The time it takes for the bias to go away goes roughly like $\frac{3}{1-\beta}$ . Thus, the larger $\beta$ is the longer it takes for this bias effect to go away. For $\beta=0.9$ it takes about 30 iterations, and for $\beta=0.999$ it takes about 3000 iterations.

In the context of machine learning though, it doesn’t really make much of a difference when you’re training for many thousands of iterations anyway. To see why, suppose you have a modest dataset of 10,000 observations. If you train this using a mini-batch size of 32, that gives about 312 iterations per epoch. Training for only 10 epochs then already puts you over 3000 iterations. Thus, unless you’re in a scenario where you can train your data very quickly (e.g. transfer learning), the bias correction probably won’t be important to you. It is thus not uncommon in practice to ignore bias correction when implementing EWMA in machine learning algorithms.

Now, the Adam algorithm uses EWMA to estimate the first and second order moment estimates of the objective function gradient $\nabla f(\theta)$ . Let us then briefly review what the moment of a random variable is.

Recall that the $n^{th}$ moment $\mu_n$ of a random variable $X$ is defined by

$\mu_n = E(X^n).$

We can see then that the first moment is just the expectation $\mu = E(X)$ , and the second moment is the uncentered variance

$\mu_2 = \mu^2 + var(X).$

For a random vector $X \in \mathbb{R}^n$ , we can extend the definition by defining the expectation component-wise by

$(\mu)_i = E(X_i),$

and the second moment component-wise by

$(\mu_2)_{ij} = E\big((XX^T)_{ij}\big).$

Back to Adam again, denote the gradient $\nabla f(\theta)$ by $g$ and the element-wise square of the gradient by $g^2$ . We then take an EWMA of each of these using smoothing parameters $\beta_1, \beta_2$ :

$m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t$ (momentum)

$v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2$ (RMSProp)

In practice, it’s common to take $\beta_1=0.9$ and $\beta_2=0.999$ , which from the above discussion you can see favors high smoothing. We can now state the Adam parameter update formally:

$\theta_t = \theta_{t-1} + \frac{\hat m_t}{\sqrt{\hat v_t}+\varepsilon}.$

Note that the bias corrected terms are included in the update! This is because the authors of the paper did so, not because it’s usually done in practice, especially for the momentum term $m_t$ . Also note the presence of the $\varepsilon$ . This is included to prevent numerical instability in the denominator, and is typically fixed in advance to a very small number, usually $\varepsilon = 10^{-8}$ . You can think of this as a form of Laplace smoothing if you wish.

The ratio $\frac{m_t}{\sqrt{v_t}}$ is used to provide an estimate of the ratio of moments $\frac{E(g)}{\sqrt{E(g^2)}}$ , which can be thought of as a point estimate of the best direction in which to descent and the best step size to take. Note that these are ratios of vectors, meaning that means that the divisions are assumed to be done component-wise.

We thus now have a “smoother” version of AdaGrad that allows for robustness in the presence of the noise inherent in SGD. Whether the algorithm holds in practice is a question that has repeatedly been validated in numerous deep learning applications. Whether this actually helps in theory leads to a discussion of the algorithm’s convergence “guarantees”.

Convergence (Colin Shea-Blymyer)

The proof of convergence for this algorithm is very long, and I fear that we won’t gain much from going through it step-by-step. Instead, we’ll turn our attention to an analysis of the regret bounds for this algorithm.

To begin, we’ll look at what regret means in this instance. Formally, regret is defined as

$R(T) = \sum\limits_{t=1}^T[f_t(\theta_t)-f_t(\theta^*)].$

In English, that represents the sum how far every step of our optimization has been from the optimal point. A high regret means our optimization has not been very efficient.

Next we’ll define $g_t$ as the gradient of our function at the point we’ve reached in our algorithm at step $t$ , and $g_{t,i}$ as the $i^{th}$ element of that gradient. We’ll use slicing on these gradients to define

$g_{1:t,i} = [g_{1,i}, g_{2,i}, ..., g_{t,i}].$

That is, a vector that contains the $i^{th}$ element of all gradients we’ve seen. We’ll also define $\gamma$ as $\frac{\beta_1^2}{\sqrt[]{\beta_2}}$ , which is a ratio of the of the decay of the importance of the first and second moments, squared and square-rooted, respectively. Further, $\lambda$ represents the exponential decay rate of $\beta_{1,t}$ .

The next step is to make some assumptions. First, assume the gradients of our function $f_t$ are bounded thus: $||\nabla f_t(\theta)||_2 \leq G$ , and $||\nabla f_t(\theta)||_\infty \leq G_\infty$ . Second, we assume a bound on the distance between any two points discovered by Adam:

$||\theta_n-\theta_m||_2 \leq D,$

$||\theta_n-\theta_m||_\infty \leq D_\infty.$

Finally, we define some ranges for our parameters: $\beta_1, \beta_2 \in [0,1)$ , and $\frac{\beta_1^2}{\sqrt{\beta_2}} < 1$ ; the learning rate at a given step $t$ is $\alpha_t = \frac{\alpha}{\sqrt{t}}$ ; finally, $\beta_{1,t} = \beta_1\lambda^{t-1}$ for $\lambda \in (0,1).$

Now we are armed to tackle the guarantee given for all $T \leq 1$ :

$R(T)\leq\frac{D^2}{2\alpha(1\beta_1)}\sum\limits_{i=1}^d\sqrt{T\hat{v}_{T,i}}+\frac{\alpha(1+\beta_1)G_\infty}{(1-\beta_1)\sqrt{1-\beta_2}(1-\gamma)^2}\sum\limits_{i=1}^d||g_{1:T,i}||_2+\sum\limits_{i=1}^d\frac{D_\infty^2G_\infty\sqrt{1-\beta_2}}{2\alpha(1-\beta_1)(1-\lambda)^2}.$

To make analysis of this easier, we’ll refer to specific terms in this inequality as such:

$R(T)\leq A B + C D + E$

Allowing each summation, and fraction without summation be a separate term.

Term $A$ is saying that a large maximum distance between points discovered by Adam can allow for a larger regret, but can be tempered by a large learning rate, and a smaller decay on the first moment. This is scaled by $B$ . Recall that $\hat{v}$ is the bias-corrected second moment estimate, so $B$ refers to the amount of variance in the function, scaled by the step number – more variance allows for more regret, especially in the later iterations of our method. $C$ has a lot to say.

We’ll start with the numerator: the learning rate, the decay of the first moment, and the maximum Chebyshev magnitude of our gradients – all aspects that allow for a larger regret when endowed with large values. In the denominator we have subtractive terms, so to maximize regret, the decay of the second and first moments, and (something like) the ratio between them should all be small. $D$ scales $C$ much in the same way $B$ scaled $A$ – instead of referring to the variance (the second moment), as $B$ does, $D$ is looking at the magnitudes of vectors formed by piecing together all previous gradients.

This, for me, is the hardest part to gain an intuition of. Finally, we find ourselves at $E$ . This piece is tricky because it’s opaque as to what the index for the summation refers to. Disregarding that, however, we see the maximum (Chebyshev) distance between points discovered (squared) multiplying the maximum (Chebyshev) norm of the gradients, multiplying a term that was in the denominator in $C$ – one less the decay rate on the second moment. In the denominator of $E$ we see the first bit of the denominator of $A$ – the learning rate, and one less the decay rate on the first moment, and one less the decay of the decay of the first moment (squared).

Looking back through this, we can start to see how certain terms effect how large the regret of the algorithm can be: the $(1-\beta_1)$ term is never found in the numerator, though $(1+\beta_1)$ is, suggesting that high values of $\beta_1$ lead to lower values of $R(T)$ . Inversely, $D$ and $G$ are never found in the denominator, clearly stating that smaller bounds on the distances and gradients lead to smaller regret values.

Finally, by accepting that

$\sum\limits_{i=1}^d||g_{1:T,i}||_2 \leq dG_\infty \sqrt{T},$

we find that $\frac{R(T)}{T}=O(\frac{1}{\sqrt{T}})$ . This allows us to say that the regret of Adam converges to 0 in the limit as $T\rightarrow\infty$ .

Natural Gradient Explained

In machine learning (supervised learning), we train a model by minimizing a loss function that outputs the difference between our prediction given a data point and the true label of that data point. Learning is cast as an optimization problem and often we use gradient descent or its variants to seek solution to this problem.

In the previous post we learnt about Gradient Descent, Newton’s method and LBFGS optimization techniques. In this post we will cover natural gradient, its formulation, usage and applications in machine learning.

To understand natural gradient, we need to revise our understanding of distance. We define the distance between two points $x, y \in \mathbb{R}^n$ in Euclidean space as

$dist(x, y) = \sqrt{\sum_{i = 1}^{n} {(x_i - y_i)}^2}$

This distance measure is not appropriate if our function of interest lies in a different geometric space other than the Euclidean space. Natural gradient employs this property by giving the distance between two points $x, y \in \mathbb{R}^n$ that lie in a Riemannian space as

$dist(x, y) = \sqrt{\sum_{i = 1}^{n} g_i(x,y){(x_i - y_i)}^2}$

where $g_i$ is the ith entry of the Riemannian metric tensor $G(x,y)$ (a positive definite matrix of size n x n)

The Riemannian metric tensor that is used in natural gradient formulation is the Fisher information matrix

$F_{\theta} = \nabla_{\hat\theta}^2 \textit{KL}(\hat\theta \quad || \quad \theta)|_{\hat\theta = \theta}$

Fisher information matrix is the second derivative of the KL-divergence. For anyone familiar with statistics, KL-divergence is a measure to determine how close a probability distribution is from another probability distribution.

Putting it all together, recall for the optimization problem $\min_{x \in \mathbb{R}} f(x)$ , the update rule using gradient descent is

$x^{(k+1)} = x^{(k)} - t^{(k)} \nabla f(x)$

For natural gradient, we update the parameters of our function using

$x^{(k+1)} = x^{(k)} - t^{(k)} F^{-1} \nabla f(x)$

where $F^{-1}$ is the inverse of the Fisher information matrix. Does this remind you of something you have seen before? Yes, this update rule is identical to that of the Newton method with the only difference being that $F^{-1}$ in Newton is the inverse of the Hessian matrix of $f(x)$ , also natural gradient does not assume that $f(x)$ is approximately locally-quadratic.

Now that we have learnt what natural gradient is and how it is formulated, we ask the question why isn’t this method popular in machine learning and what problems are they good for solving? In practice, natural gradient method is applied to a variety of problems, variational inference, deep neural networks, reinforcement learning and in some cases it performs better than conventional methods e.g. stochastic gradient descent. The main limitation of natural gradient method is that we need to know the Riemannian structure of the parameter space of our function in order to derive its update rule and deriving the algorithm for that can be complex. Also, applying the algorithm can be computationally intensive.

In this post, we have learnt about natural gradient and that it performs better than conventional optimization methods when applied to some problems. I will strongly encourage anyone seeking a more in depth coverage of natural gradient adaptation to check out this paper, or alternatively, this paper to get a concise explanation with mathematical derivations.