February 2018 – Optimization in Machine Learning

Subgradient Method and Stochastic Gradient Descent

Subgradient Method

Subgradient method is the basic optimization algorithm for convex nondifferentiable functions. First, let’s see what a subgradient is. A subgradient is a generalization of the gradient for nondifferentiable functions. For simplicity, let’s elaborate it in a one-dimensional space. The gradient of a function at a certain point is the slope of the tangent line at that point.

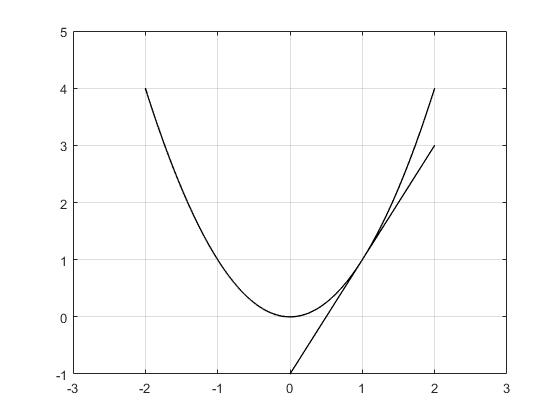
However, for nondifferentiable functions, there is no unique gradient at nondifferentiable points. Instead, there are subgradients $g$ which satisfy the following condition:

$f(y)\geq J(x) +g^T(y-x)$ for all y.

All vectors $g$ that satisfy this condition are called subgradients of the function J at point x.

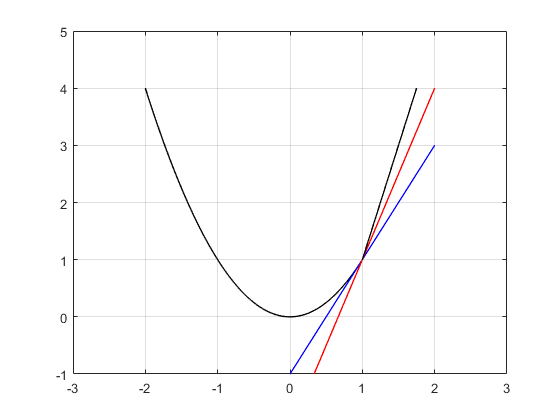
Fig. 2: Slopes of both blue and red line are the subgradients of the nondifferentiable function in the breaking point.

In Fig. 2, you can see that slopes of both blue and red lines are subgradients of the function at $x=1$ .

Now assume that our goal is to minimize the cost function $f(x)$ . The update algorithm is simply

$x^{(k+1)}=x^{(k)}-\alpha_k g^{(k)},$

where $\alpha_k$ is subgradient of $f(x)$ at point $x^{(k)}$ .

However, the subgradient direction is not always a descent direction (can you think of an example?), so we have to keep track of the smallest objective function value that we have reached so far(i.e. iteration $k$ ):

$f^k_{best}=\min \{f(x^{(1)}),\cdots,f(x^{(k)})\}$

The proof of convergence for this algorithm depends on three conditions:

The function $f(x)$ is a convex function. However, it is not necessarily strongly convex.
The size of the subgradient is bounded, i.e, $\|g^{(k)}\|_2 \leq G$ for all $k$ . For example, if the function $f(x)$ is Lipschitz continuous, then its subgradient is bounded.
The distance of the initial point to the optimal set is bounded by $R$ , i.e., $\|x^{(1)}-x^*\leq R\|_2$ .

With the aforementioned conditions, it is shown that the distance between best point found so far $f^k_{best}$ of the algorithm with the optimum value $f^*$ is bounded, i.e.,

$f^k_{best}-f^* \leq \frac{R^2+G^2\sum_{i=1}^k \alpha_i^2}{2 \sum_{i=1}^k \alpha_i}$

Now, depending on the step size $\alpha_i$ , we find different values for the bound. Two step sizes that we went through their detail in the class were:

Constant step size $\alpha_i=\alpha$ : which is a positive constant. In this case, we will have $f^k_{best}-f^* \leq \frac{R^2+G^2 k \alpha^2}{2 k \alpha}$ . As $k$ goes to infinity, the bound converges to $G^2 \alpha/2$ .
Square summable but not summable $\sum_{k=1}^\infty \alpha_k^2<\infty$ , $\sum_{k=1}^\infty \alpha_k=\infty$

We showed that the convergence rate in both cases are sublinear with the definition here.

Also, we discussed in class that if the number of iterations is determined, i.e., we want to reach the best we can in $k$ iterations, then the best possible bound that we can get with any step size is:

$f^k_{best}-f^* \leq \frac{R G}{\sqrt{k}}$

Using this bound, we found that if we want to reduce the gap between the current objective value and the optimal objective by a factor of 1000, we need $10^6$ iterations. To compare it with the gradient descent method, we have to note that if $\frac{m}{M}=0.5$ , then it only needs 10 iterations in gradient descent. However, this gradient descent convergence rate is for strongly convex case only.

Stochastic Gradient Descent

We have seen that we can use standard gradient descent given a convex function and its gradient. We discussed earlier in this section that we can use subgradient descent given a convex function with undefined gradient and its subgradient. What approach is appropriate when we are given a convex function with a stochastic gradient?

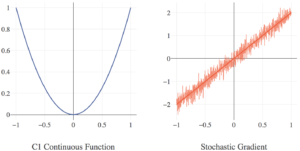
Stochastic gradient descent (SGD) is a term used to describe the application of classic gradient descent and subgradient methods when only a stochastic estimate of the true (sub)gradient is available.

To get a better feel for what this means and why this is useful, imagine the following two motivating examples. First, consider the training of a neural network (NN) when we have millions of training samples. The huge number of training samples causes the calculation of the gradient to be very expensive, making training slow. We could randomly select a subset of training samples (say, 1000 of them) and compute a gradient with respect to only that sample. We assume (and in this case, know) that the gradient estimate generated from a sample will behave like the true gradient on average and still point us in a general descent direction.

In another example consider a black box optimization problem, meaning that the optimization algorithm only has access to actual function values *without* gradient information. At first glance, it may seem like gradient descent methods cannot be used for this problem. However, if we assume that the underlying function has some amount of “smoothness” and randomly sample function values near the current iterate, we can use a least squares fit to estimate the gradient.

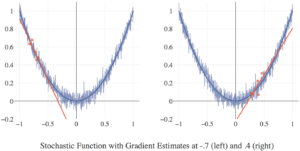
In general, the formal assumption for any SGD method is that the optimization algorithm has access to an estimate $\hat{g}$ for the true (sub)gradient $\nabla f$ at every point $x$ , which satisfies

${\mathbb{E}\left(\hat{g}(x)\right)} = \nabla f(x),$

where $\mathbb{E}\left(\hat{g}(x)\right)$ denotes the expected value of $\hat{g}$ at $x$ .

Using $\hat{g}$ as a proxy for $\nabla f$ , we can perform standard (sub)gradient descent in order to converge in expected value to the true minimum. That is, we can use the “vanilla” SGD update

$x^{(k+1)} = x^{(k)} - \alpha^{(k)} \hat{g}(x^{(k)})$

where $\alpha^{(k)}$ is the step size.

We see two convergence proofs for this vanilla SGD. The first leverages an inductive argument to show that for a strongly convex differentiable function $f$, after $t$ iterations using a diminishing step size $\alpha^{(k)} = \frac{C}{k}$ , the expected error in function value is given by

$\mathbb{E}(f(x^{(t)}) - f(x^*)) \approx \mathcal{O}(\frac{1}{t})$

where $x^*$ is the true optimal value for $x$ .

In a slight modification, often called “robust” SGD, we relax the assumptions so that $f$ need only be convex with a subgradient. Now, using a constant step size $\alpha^{(k)} = \alpha$ , robust SGD can be proven to converge to some neighborhood of the true minima $x^*$ with a radius proportional to $\alpha$ at a rate of $\mathcal{O}(\frac{1}{\sqrt{t}})$ . It follows, that for a general function, it is good practice to begin SGD with a constant step size, then diminish the step size whenever the algorithm seems to have stalled in its progress.

Gradient Descent, Newton’s Method, and LBFGS

In the first few sessions of the course, we went over gradient descent (with exact line search), Newton’s Method, and quasi-Newton methods. For me, and many of the students, this was the first time I had sat down to go over the convergence guarantees of these methods and how they are proven.

Generally, we were examining descent methods that aim to solve optimizations of the form

$\min_{x \in \mathbb{R}} f(x)$

by iteratively trying input vectors in a sequence defined by

$x^{(k+1)} = x^{(k)} + t^{(k)} \Delta x$ .

For the analyses we studied so far, we assume the function is strongly convex, meaning that there exists some constant $m$ for which

$f(y) \le f(x) + \nabla f(x)^\top (y - x) + \frac{m}{2} || y - x ||^2$ ,

and there is another constant $M$ such that

$f(y) \ge f(x) + \nabla f(x)^\top (y - x) + \frac{M}{2} || y - x ||^2$ .

In other words, the function can be upper and lower bounded by quadratic functions.

Gradient Descent

We first went over the proof in Boyd and Vanderberghe’s textbook on convex optimization for gradient descent. The approach they used to show the convergence rate of gradient descent was to bound the improvement each iteration, which shows that the gap between the current objective value and the optimal objective value shrinks by a constant factor each iteration. This constant factor shrinkage is known as linear convergence. This type of analysis results in a bound of the form

$f(x) - p* \le c^k (f(x^{(0)}) - p*)$ ,

where $c = 1 - m / M$ is considered a constant, and $p*$ is the value of $f$ at the optimum. Each individual step to arrive at this bound were fairly easy to understand, but I found it a bit hard to see how the original analysts decided what steps to take. Did they start with the linear convergence rate and work backwards? Or did they try different manipulations of the strong convexity conditions until they reached a linear rate? I hope as we study more proofs in the semester that I, and the students, start to gain a better intuition about how to do these proofs ourselves when faced with a new method.

Newton’s Method

We continued with the Boyd & Vanderberghe book, looking at its discussion of Newton’s Method (with backtracking). Many of us in the class had the rough idea that Newton’s Method, because it uses second-order information, achieves a quadratic convergence rate, and the analysis does confirm that.

The backtracking Newton Update is

$x^{(k+1)} = x^{(k)} - t^{(k)} \nabla^2 f(x)^{-1} \nabla f(x)$ ,

where the step size $t^{(k)}$ shrinks until [to-do: describe backtracking condition].

The analysis adds another assumption about $f$ : that its Hessian is Lipschitz continuous:

$||\nabla^2 f(x) - \nabla^2 f(y)|| \le L ||x - y||$ .

The convergence analysis is broken into two phases, one where the backtracking search backtracks, and the other where the full Newton Step is used. During the phase with the full Newton Step, it is shown that the error is bounded by a rapidly shrinking constant:

$f(x^{(l)}) - p* \le \frac{2m^3}{L^2} \left( \frac{1}{2} \right)^{2^{l - k + 1}}$ ,

where $k$ is the step at which we enter this second phase. This is the quadratically converging phase of Newton’s Method. The key is then how quickly we enter the second phase. The eventual bound on how many steps it takes to enter the second phase is

$k \le \frac{M^2 L^2 / m^5}{\alpha \beta \min\{1, 9 (1 - 2 \alpha)^2 \}} (f(x^{(0)}) - p*)$ .

In this formula $\alpha$ and $\latex beta$ are constant parameters of the backtracking line search, so the number of iterations necessary to start the quadratically converging phase is a constant scaling of the initial error.

LBFGS

Newton’s Method is great, but each iteration is rather expensive because it involves the computation of the Hessian and inverting it. For high-dimensional problems, this can make Newton’s Method practically unusable. Our last topic of this block of classes was on one of the more famous quasi-Newton methods. We decided to read the highly cite paper [to-do paper title], but we were surprised as a class to discover that this paper is more of an empirical study of LBFGS in comparison to other quasi-Newton approaches. So we supplemented with other resources, like Vandenberghe’s slides.

We were surprised in the proof presented in Liu and Nocedal’s paper that they prove LBFGS to be a linearly converging method. If LBFGS is not provably faster than gradient descent, it’s not clear why anyone would use it. However, we hypothesized as a class that there may be other proofs elsewhere that show super-linear convergence, because many of us thought we had seen LBFGS listed as a super-linear algorithm. We’ll certainly look into this later as a class.

We spent time in class going over the secant condition that LBFGS, and BFGS, uses to approximate the Hessian. The key idea we had to understand is that the secant method can be viewed as a linear approximation of the Hessian analogous to making a linear approximation of the gradient by measuring the function value at two points. One measures the gradient at two locations $\nabla f(x)$ and $\nabla f(y)$ , and the secant condition is

$H(x - y) = \nabla f(x) - \nabla f(y)$ .

The BFGS method then iteratively projects the previous Hessian approximation onto the space of Hessian approximations that agree with this condition, which is reasonable if you believe the Hessian does not change much. LBFGS instead only stores the previous $m$ gradients and estimates the Hessian using those.

We also puzzled over how LBFGS can avoid the quadratic cost of either storing or computing the approximate Hessian. As a class, we were initially confused because most formulas for the approximate Hessian include outer product terms involving the differences between the input vectors and the gradients, e.g.,

$\underbrace{(x^{(j)} - x^{(j - 1)})}_{s^j} ~ \underbrace{(\nabla f(x^{(j)}) - \nabla f(x^{(j - 1)}))^\top}_{y_j}$ ,

where $s_j$ and $y_j$ are the shorthand used to describe these difference vectors in the slides. Based on the existence of these outer products, it appears as if an $O(n^2)$ cost is unavoidable, when all the literature says the memory and running time costs are $O(mn)$ .

The key insight to why we can avoid the quadratic cost—of even thinking about the full-sized Hessian—is that in all cases of these outer products, they are eventually right multiplied by yet another vector of length $n$ . We then have products of length- $n$ vectors that look like

$\underbrace{a b^\top}_{n \times n} \underbrace{c}_{n \times 1}$ ,

which can be computed much more efficiently by first multiplying the dot product on the right:

$\underbrace{a}_{n \times 1} \underbrace{b^\top c}_{1 \times 1}$ .

Concluding Thoughts

One of my goals with looking at these foundational methods first was to gain an intuition of how to prove convergence of more sophisticated optimization approaches. To do so, I was hoping to find nice patterns of proof techniques. I’m not certain that I did that, personally, with these three analyses. Parts of the analyses were analogous to each other, but overall, their convergence proofs seemed rather different to me. Perhaps as we see more analyses throughout the semester, we’ll start to recognize patterns more.

It’s interesting to have sat down to really dig into these methods, since so much of what I know as a machine learning researchers comes from “mythology” about these methods. One important note is the strength of the assumptions underlying the convergence guarantees. We often use these methods and variants on functions that may not be strongly convex or convex at all. These misuses of these algorithms will naturally occur. “When all you have is a hammer…” From spending three (and a half) classes looking at these convergence guarantees, I don’t yet have a clear idea of what we can say theoretically when these assumptions are violated.

Hello world!

This semester, I am teaching a graduate seminar course on optimization in machine learning. This blog will chronicle our exploration of the literature on this topic, including the results we find most interesting, the proof techniques that we want to highlight, and questions we have (whether because we couldn’t decipher the answer from the literature or because they are truly open questions). Most posts will be co-written by the students, but I’ll open with the first post on what we covered in the first few classes.