Optimization in Machine Learning

Adam

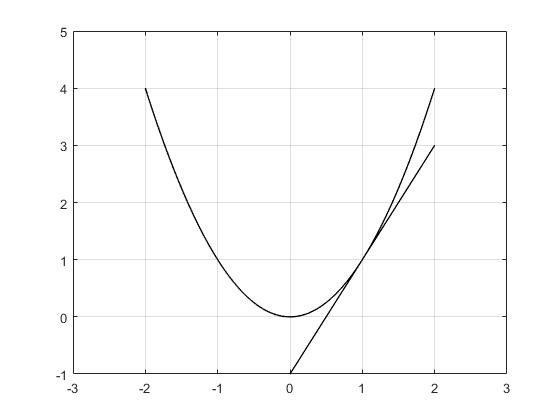
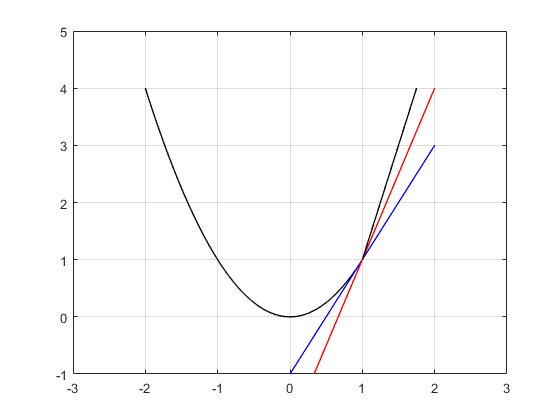
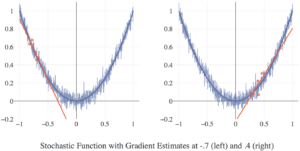
This post presents a summary of the background and class discussion on the Adam (adaptive moment estimation) algorithm. The primary source for this discussion was the original Adam paper. Adam is quite possibly the most popular optimization algorithm being used today in machine learning, particularly in deep learning.

Background (Ryan Kingery)

Adam can be thought of as a generalization of stochastic gradient descent (SGD). It essentially combines three popular additions to SGD into one algorithm: AdaGrad, Nesterov momentum, and RMSProp.

Adam = AdaGrad + momentum + RMSProp

Recall from a previous post that AdaGrad modifies SGD by allowing for variable learning rates that can hopefully take advantage of the curvature of the objective function to allow for faster convergence. With Adam we extend this idea by using moving averages of the gradient moment estimates to smooth the stochastic descent trajectory. The idea is that smoothing this trajectory should speed up convergence by making Adam converge more like batch gradient descent, but without the need of using the entire dataset.

To discuss momentum and RMSProp we must recall the definition of an exponentially weighted moving average (EWMA), also called exponential smoothing or infinite impulse response filtering. Suppose we have a random sample $x_1,\cdots,x_T$ of time-ordered data. An EWMA generates a new sequence $m_1,\cdots,m_T$ defined by

$m_t = \beta m_{t-1} + (1-\beta)x_t = (1-\beta) \sum_{i=1}^t \beta^{t-i}x_i.$

The hyperparameter $0 \leq \beta \leq 1$ is called a smoothing parameter. Intuitively, the EWMA is a way of smoothing time-ordered data. When $\beta \approx 0$ , the EWMA sequence depends only on the current value of $x_t$ , which just gives the original non-smoothed sequence back. When $\beta \approx 1$ , the EWMA doesn’t depend at all on the current value $x_t$ , which results in a constant value for all $m_t$ .

The EWMA is useful when we’re given noisy data and would like to filter out some of the noise to allow for better estimation of the underlying process. We thus in practice tend to favor higher values of $\beta$ , usually 0.9 or higher. It is precisely this idea that momentum and RMSProp exploit. Before mentioning this, though, a minor point.

It turns out that the EWMA tends to produce bias estimates for the early values $x_t$ . When the process hasn’t generated enough data yet, EWMA sets all the remaining values it needs to 0, which tends to bias the earlier part of the EWMA sequence towards 0. To fix this problem, one can use instead a bias-corrected EWMA defined by

$\hat m_t = \frac{m_t}{1-\beta^t}.$

One might naturally ask whether this bias correction term is something to worry about in practice, and the answer, of course, is it depends. The time it takes for the bias to go away goes roughly like $\frac{3}{1-\beta}$ . Thus, the larger $\beta$ is the longer it takes for this bias effect to go away. For $\beta=0.9$ it takes about 30 iterations, and for $\beta=0.999$ it takes about 3000 iterations.

In the context of machine learning though, it doesn’t really make much of a difference when you’re training for many thousands of iterations anyway. To see why, suppose you have a modest dataset of 10,000 observations. If you train this using a mini-batch size of 32, that gives about 312 iterations per epoch. Training for only 10 epochs then already puts you over 3000 iterations. Thus, unless you’re in a scenario where you can train your data very quickly (e.g. transfer learning), the bias correction probably won’t be important to you. It is thus not uncommon in practice to ignore bias correction when implementing EWMA in machine learning algorithms.

Now, the Adam algorithm uses EWMA to estimate the first and second order moment estimates of the objective function gradient $\nabla f(\theta)$ . Let us then briefly review what the moment of a random variable is.

Recall that the $n^{th}$ moment $\mu_n$ of a random variable $X$ is defined by

$\mu_n = E(X^n).$

We can see then that the first moment is just the expectation $\mu = E(X)$ , and the second moment is the uncentered variance

$\mu_2 = \mu^2 + var(X).$

For a random vector $X \in \mathbb{R}^n$ , we can extend the definition by defining the expectation component-wise by

$(\mu)_i = E(X_i),$

and the second moment component-wise by

$(\mu_2)_{ij} = E\big((XX^T)_{ij}\big).$

Back to Adam again, denote the gradient $\nabla f(\theta)$ by $g$ and the element-wise square of the gradient by $g^2$ . We then take an EWMA of each of these using smoothing parameters $\beta_1, \beta_2$ :

$m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t$ (momentum)

$v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2$ (RMSProp)

In practice, it’s common to take $\beta_1=0.9$ and $\beta_2=0.999$ , which from the above discussion you can see favors high smoothing. We can now state the Adam parameter update formally:

$\theta_t = \theta_{t-1} + \frac{\hat m_t}{\sqrt{\hat v_t}+\varepsilon}.$

Note that the bias corrected terms are included in the update! This is because the authors of the paper did so, not because it’s usually done in practice, especially for the momentum term $m_t$ . Also note the presence of the $\varepsilon$ . This is included to prevent numerical instability in the denominator, and is typically fixed in advance to a very small number, usually $\varepsilon = 10^{-8}$ . You can think of this as a form of Laplace smoothing if you wish.

The ratio $\frac{m_t}{\sqrt{v_t}}$ is used to provide an estimate of the ratio of moments $\frac{E(g)}{\sqrt{E(g^2)}}$ , which can be thought of as a point estimate of the best direction in which to descent and the best step size to take. Note that these are ratios of vectors, meaning that means that the divisions are assumed to be done component-wise.

We thus now have a “smoother” version of AdaGrad that allows for robustness in the presence of the noise inherent in SGD. Whether the algorithm holds in practice is a question that has repeatedly been validated in numerous deep learning applications. Whether this actually helps in theory leads to a discussion of the algorithm’s convergence “guarantees”.

Convergence (Colin Shea-Blymyer)

The proof of convergence for this algorithm is very long, and I fear that we won’t gain much from going through it step-by-step. Instead, we’ll turn our attention to an analysis of the regret bounds for this algorithm.

To begin, we’ll look at what regret means in this instance. Formally, regret is defined as

$R(T) = \sum\limits_{t=1}^T[f_t(\theta_t)-f_t(\theta^*)].$

In English, that represents the sum how far every step of our optimization has been from the optimal point. A high regret means our optimization has not been very efficient.

Next we’ll define $g_t$ as the gradient of our function at the point we’ve reached in our algorithm at step $t$ , and $g_{t,i}$ as the $i^{th}$ element of that gradient. We’ll use slicing on these gradients to define

$g_{1:t,i} = [g_{1,i}, g_{2,i}, ..., g_{t,i}].$

That is, a vector that contains the $i^{th}$ element of all gradients we’ve seen. We’ll also define $\gamma$ as $\frac{\beta_1^2}{\sqrt[]{\beta_2}}$ , which is a ratio of the of the decay of the importance of the first and second moments, squared and square-rooted, respectively. Further, $\lambda$ represents the exponential decay rate of $\beta_{1,t}$ .

The next step is to make some assumptions. First, assume the gradients of our function $f_t$ are bounded thus: $||\nabla f_t(\theta)||_2 \leq G$ , and $||\nabla f_t(\theta)||_\infty \leq G_\infty$ . Second, we assume a bound on the distance between any two points discovered by Adam:

$||\theta_n-\theta_m||_2 \leq D,$

$||\theta_n-\theta_m||_\infty \leq D_\infty.$

Finally, we define some ranges for our parameters: $\beta_1, \beta_2 \in [0,1)$ , and $\frac{\beta_1^2}{\sqrt{\beta_2}} < 1$ ; the learning rate at a given step $t$ is $\alpha_t = \frac{\alpha}{\sqrt{t}}$ ; finally, $\beta_{1,t} = \beta_1\lambda^{t-1}$ for $\lambda \in (0,1).$

Now we are armed to tackle the guarantee given for all $T \leq 1$ :

$R(T)\leq\frac{D^2}{2\alpha(1\beta_1)}\sum\limits_{i=1}^d\sqrt{T\hat{v}_{T,i}}+\frac{\alpha(1+\beta_1)G_\infty}{(1-\beta_1)\sqrt{1-\beta_2}(1-\gamma)^2}\sum\limits_{i=1}^d||g_{1:T,i}||_2+\sum\limits_{i=1}^d\frac{D_\infty^2G_\infty\sqrt{1-\beta_2}}{2\alpha(1-\beta_1)(1-\lambda)^2}.$

To make analysis of this easier, we’ll refer to specific terms in this inequality as such:

$R(T)\leq A B + C D + E$

Allowing each summation, and fraction without summation be a separate term.

Term $A$ is saying that a large maximum distance between points discovered by Adam can allow for a larger regret, but can be tempered by a large learning rate, and a smaller decay on the first moment. This is scaled by $B$ . Recall that $\hat{v}$ is the bias-corrected second moment estimate, so $B$ refers to the amount of variance in the function, scaled by the step number – more variance allows for more regret, especially in the later iterations of our method. $C$ has a lot to say.

We’ll start with the numerator: the learning rate, the decay of the first moment, and the maximum Chebyshev magnitude of our gradients – all aspects that allow for a larger regret when endowed with large values. In the denominator we have subtractive terms, so to maximize regret, the decay of the second and first moments, and (something like) the ratio between them should all be small. $D$ scales $C$ much in the same way $B$ scaled $A$ – instead of referring to the variance (the second moment), as $B$ does, $D$ is looking at the magnitudes of vectors formed by piecing together all previous gradients.

This, for me, is the hardest part to gain an intuition of. Finally, we find ourselves at $E$ . This piece is tricky because it’s opaque as to what the index for the summation refers to. Disregarding that, however, we see the maximum (Chebyshev) distance between points discovered (squared) multiplying the maximum (Chebyshev) norm of the gradients, multiplying a term that was in the denominator in $C$ – one less the decay rate on the second moment. In the denominator of $E$ we see the first bit of the denominator of $A$ – the learning rate, and one less the decay rate on the first moment, and one less the decay of the decay of the first moment (squared).

Looking back through this, we can start to see how certain terms effect how large the regret of the algorithm can be: the $(1-\beta_1)$ term is never found in the numerator, though $(1+\beta_1)$ is, suggesting that high values of $\beta_1$ lead to lower values of $R(T)$ . Inversely, $D$ and $G$ are never found in the denominator, clearly stating that smaller bounds on the distances and gradients lead to smaller regret values.

Finally, by accepting that

$\sum\limits_{i=1}^d||g_{1:T,i}||_2 \leq dG_\infty \sqrt{T},$

we find that $\frac{R(T)}{T}=O(\frac{1}{\sqrt{T}})$ . This allows us to say that the regret of Adam converges to 0 in the limit as $T\rightarrow\infty$ .

Natural Gradient Explained

In machine learning (supervised learning), we train a model by minimizing a loss function that outputs the difference between our prediction given a data point and the true label of that data point. Learning is cast as an optimization problem and often we use gradient descent or its variants to seek solution to this problem.

In the previous post we learnt about Gradient Descent, Newton’s method and LBFGS optimization techniques. In this post we will cover natural gradient, its formulation, usage and applications in machine learning.

To understand natural gradient, we need to revise our understanding of distance. We define the distance between two points $x, y \in \mathbb{R}^n$ in Euclidean space as

$dist(x, y) = \sqrt{\sum_{i = 1}^{n} {(x_i - y_i)}^2}$

This distance measure is not appropriate if our function of interest lies in a different geometric space other than the Euclidean space. Natural gradient employs this property by giving the distance between two points $x, y \in \mathbb{R}^n$ that lie in a Riemannian space as

$dist(x, y) = \sqrt{\sum_{i = 1}^{n} g_i(x,y){(x_i - y_i)}^2}$

where $g_i$ is the ith entry of the Riemannian metric tensor $G(x,y)$ (a positive definite matrix of size n x n)

The Riemannian metric tensor that is used in natural gradient formulation is the Fisher information matrix

$F_{\theta} = \nabla_{\hat\theta}^2 \textit{KL}(\hat\theta \quad || \quad \theta)|_{\hat\theta = \theta}$

Fisher information matrix is the second derivative of the KL-divergence. For anyone familiar with statistics, KL-divergence is a measure to determine how close a probability distribution is from another probability distribution.

Putting it all together, recall for the optimization problem $\min_{x \in \mathbb{R}} f(x)$ , the update rule using gradient descent is

$x^{(k+1)} = x^{(k)} - t^{(k)} \nabla f(x)$

For natural gradient, we update the parameters of our function using

$x^{(k+1)} = x^{(k)} - t^{(k)} F^{-1} \nabla f(x)$

where $F^{-1}$ is the inverse of the Fisher information matrix. Does this remind you of something you have seen before? Yes, this update rule is identical to that of the Newton method with the only difference being that $F^{-1}$ in Newton is the inverse of the Hessian matrix of $f(x)$ , also natural gradient does not assume that $f(x)$ is approximately locally-quadratic.

Now that we have learnt what natural gradient is and how it is formulated, we ask the question why isn’t this method popular in machine learning and what problems are they good for solving? In practice, natural gradient method is applied to a variety of problems, variational inference, deep neural networks, reinforcement learning and in some cases it performs better than conventional methods e.g. stochastic gradient descent. The main limitation of natural gradient method is that we need to know the Riemannian structure of the parameter space of our function in order to derive its update rule and deriving the algorithm for that can be complex. Also, applying the algorithm can be computationally intensive.

In this post, we have learnt about natural gradient and that it performs better than conventional optimization methods when applied to some problems. I will strongly encourage anyone seeking a more in depth coverage of natural gradient adaptation to check out this paper, or alternatively, this paper to get a concise explanation with mathematical derivations.

Subgradient Method and Stochastic Gradient Descent

Subgradient Method

Subgradient method is the basic optimization algorithm for convex nondifferentiable functions. First, let’s see what a subgradient is. A subgradient is a generalization of the gradient for nondifferentiable functions. For simplicity, let’s elaborate it in a one-dimensional space. The gradient of a function at a certain point is the slope of the tangent line at that point.

However, for nondifferentiable functions, there is no unique gradient at nondifferentiable points. Instead, there are subgradients $g$ which satisfy the following condition:

$f(y)\geq J(x) +g^T(y-x)$ for all y.

All vectors $g$ that satisfy this condition are called subgradients of the function J at point x.

Fig. 2: Slopes of both blue and red line are the subgradients of the nondifferentiable function in the breaking point.

In Fig. 2, you can see that slopes of both blue and red lines are subgradients of the function at $x=1$ .

Now assume that our goal is to minimize the cost function $f(x)$ . The update algorithm is simply

$x^{(k+1)}=x^{(k)}-\alpha_k g^{(k)},$

where $\alpha_k$ is subgradient of $f(x)$ at point $x^{(k)}$ .

However, the subgradient direction is not always a descent direction (can you think of an example?), so we have to keep track of the smallest objective function value that we have reached so far(i.e. iteration $k$ ):

$f^k_{best}=\min \{f(x^{(1)}),\cdots,f(x^{(k)})\}$

The proof of convergence for this algorithm depends on three conditions:

The function $f(x)$ is a convex function. However, it is not necessarily strongly convex.
The size of the subgradient is bounded, i.e, $\|g^{(k)}\|_2 \leq G$ for all $k$ . For example, if the function $f(x)$ is Lipschitz continuous, then its subgradient is bounded.
The distance of the initial point to the optimal set is bounded by $R$ , i.e., $\|x^{(1)}-x^*\leq R\|_2$ .

With the aforementioned conditions, it is shown that the distance between best point found so far $f^k_{best}$ of the algorithm with the optimum value $f^*$ is bounded, i.e.,

$f^k_{best}-f^* \leq \frac{R^2+G^2\sum_{i=1}^k \alpha_i^2}{2 \sum_{i=1}^k \alpha_i}$

Now, depending on the step size $\alpha_i$ , we find different values for the bound. Two step sizes that we went through their detail in the class were:

Constant step size $\alpha_i=\alpha$ : which is a positive constant. In this case, we will have $f^k_{best}-f^* \leq \frac{R^2+G^2 k \alpha^2}{2 k \alpha}$ . As $k$ goes to infinity, the bound converges to $G^2 \alpha/2$ .
Square summable but not summable $\sum_{k=1}^\infty \alpha_k^2<\infty$ , $\sum_{k=1}^\infty \alpha_k=\infty$

We showed that the convergence rate in both cases are sublinear with the definition here.

Also, we discussed in class that if the number of iterations is determined, i.e., we want to reach the best we can in $k$ iterations, then the best possible bound that we can get with any step size is:

$f^k_{best}-f^* \leq \frac{R G}{\sqrt{k}}$

Using this bound, we found that if we want to reduce the gap between the current objective value and the optimal objective by a factor of 1000, we need $10^6$ iterations. To compare it with the gradient descent method, we have to note that if $\frac{m}{M}=0.5$ , then it only needs 10 iterations in gradient descent. However, this gradient descent convergence rate is for strongly convex case only.

Stochastic Gradient Descent

We have seen that we can use standard gradient descent given a convex function and its gradient. We discussed earlier in this section that we can use subgradient descent given a convex function with undefined gradient and its subgradient. What approach is appropriate when we are given a convex function with a stochastic gradient?

Stochastic gradient descent (SGD) is a term used to describe the application of classic gradient descent and subgradient methods when only a stochastic estimate of the true (sub)gradient is available.

To get a better feel for what this means and why this is useful, imagine the following two motivating examples. First, consider the training of a neural network (NN) when we have millions of training samples. The huge number of training samples causes the calculation of the gradient to be very expensive, making training slow. We could randomly select a subset of training samples (say, 1000 of them) and compute a gradient with respect to only that sample. We assume (and in this case, know) that the gradient estimate generated from a sample will behave like the true gradient on average and still point us in a general descent direction.

In another example consider a black box optimization problem, meaning that the optimization algorithm only has access to actual function values *without* gradient information. At first glance, it may seem like gradient descent methods cannot be used for this problem. However, if we assume that the underlying function has some amount of “smoothness” and randomly sample function values near the current iterate, we can use a least squares fit to estimate the gradient.

In general, the formal assumption for any SGD method is that the optimization algorithm has access to an estimate $\hat{g}$ for the true (sub)gradient $\nabla f$ at every point $x$ , which satisfies

${\mathbb{E}\left(\hat{g}(x)\right)} = \nabla f(x),$

where $\mathbb{E}\left(\hat{g}(x)\right)$ denotes the expected value of $\hat{g}$ at $x$ .

Using $\hat{g}$ as a proxy for $\nabla f$ , we can perform standard (sub)gradient descent in order to converge in expected value to the true minimum. That is, we can use the “vanilla” SGD update

$x^{(k+1)} = x^{(k)} - \alpha^{(k)} \hat{g}(x^{(k)})$

where $\alpha^{(k)}$ is the step size.

We see two convergence proofs for this vanilla SGD. The first leverages an inductive argument to show that for a strongly convex differentiable function $f$, after $t$ iterations using a diminishing step size $\alpha^{(k)} = \frac{C}{k}$ , the expected error in function value is given by

$\mathbb{E}(f(x^{(t)}) - f(x^*)) \approx \mathcal{O}(\frac{1}{t})$

where $x^*$ is the true optimal value for $x$ .

In a slight modification, often called “robust” SGD, we relax the assumptions so that $f$ need only be convex with a subgradient. Now, using a constant step size $\alpha^{(k)} = \alpha$ , robust SGD can be proven to converge to some neighborhood of the true minima $x^*$ with a radius proportional to $\alpha$ at a rate of $\mathcal{O}(\frac{1}{\sqrt{t}})$ . It follows, that for a general function, it is good practice to begin SGD with a constant step size, then diminish the step size whenever the algorithm seems to have stalled in its progress.

Gradient Descent, Newton’s Method, and LBFGS

In the first few sessions of the course, we went over gradient descent (with exact line search), Newton’s Method, and quasi-Newton methods. For me, and many of the students, this was the first time I had sat down to go over the convergence guarantees of these methods and how they are proven.

Generally, we were examining descent methods that aim to solve optimizations of the form

$\min_{x \in \mathbb{R}} f(x)$

by iteratively trying input vectors in a sequence defined by

$x^{(k+1)} = x^{(k)} + t^{(k)} \Delta x$ .

For the analyses we studied so far, we assume the function is strongly convex, meaning that there exists some constant $m$ for which

$f(y) \le f(x) + \nabla f(x)^\top (y - x) + \frac{m}{2} || y - x ||^2$ ,

and there is another constant $M$ such that

$f(y) \ge f(x) + \nabla f(x)^\top (y - x) + \frac{M}{2} || y - x ||^2$ .

In other words, the function can be upper and lower bounded by quadratic functions.

Gradient Descent

We first went over the proof in Boyd and Vanderberghe’s textbook on convex optimization for gradient descent. The approach they used to show the convergence rate of gradient descent was to bound the improvement each iteration, which shows that the gap between the current objective value and the optimal objective value shrinks by a constant factor each iteration. This constant factor shrinkage is known as linear convergence. This type of analysis results in a bound of the form

$f(x) - p* \le c^k (f(x^{(0)}) - p*)$ ,

where $c = 1 - m / M$ is considered a constant, and $p*$ is the value of $f$ at the optimum. Each individual step to arrive at this bound were fairly easy to understand, but I found it a bit hard to see how the original analysts decided what steps to take. Did they start with the linear convergence rate and work backwards? Or did they try different manipulations of the strong convexity conditions until they reached a linear rate? I hope as we study more proofs in the semester that I, and the students, start to gain a better intuition about how to do these proofs ourselves when faced with a new method.

Newton’s Method

We continued with the Boyd & Vanderberghe book, looking at its discussion of Newton’s Method (with backtracking). Many of us in the class had the rough idea that Newton’s Method, because it uses second-order information, achieves a quadratic convergence rate, and the analysis does confirm that.

The backtracking Newton Update is

$x^{(k+1)} = x^{(k)} - t^{(k)} \nabla^2 f(x)^{-1} \nabla f(x)$ ,

where the step size $t^{(k)}$ shrinks until [to-do: describe backtracking condition].

The analysis adds another assumption about $f$ : that its Hessian is Lipschitz continuous:

$||\nabla^2 f(x) - \nabla^2 f(y)|| \le L ||x - y||$ .

The convergence analysis is broken into two phases, one where the backtracking search backtracks, and the other where the full Newton Step is used. During the phase with the full Newton Step, it is shown that the error is bounded by a rapidly shrinking constant:

$f(x^{(l)}) - p* \le \frac{2m^3}{L^2} \left( \frac{1}{2} \right)^{2^{l - k + 1}}$ ,

where $k$ is the step at which we enter this second phase. This is the quadratically converging phase of Newton’s Method. The key is then how quickly we enter the second phase. The eventual bound on how many steps it takes to enter the second phase is

$k \le \frac{M^2 L^2 / m^5}{\alpha \beta \min\{1, 9 (1 - 2 \alpha)^2 \}} (f(x^{(0)}) - p*)$ .

In this formula $\alpha$ and $\latex beta$ are constant parameters of the backtracking line search, so the number of iterations necessary to start the quadratically converging phase is a constant scaling of the initial error.

LBFGS

Newton’s Method is great, but each iteration is rather expensive because it involves the computation of the Hessian and inverting it. For high-dimensional problems, this can make Newton’s Method practically unusable. Our last topic of this block of classes was on one of the more famous quasi-Newton methods. We decided to read the highly cite paper [to-do paper title], but we were surprised as a class to discover that this paper is more of an empirical study of LBFGS in comparison to other quasi-Newton approaches. So we supplemented with other resources, like Vandenberghe’s slides.

We were surprised in the proof presented in Liu and Nocedal’s paper that they prove LBFGS to be a linearly converging method. If LBFGS is not provably faster than gradient descent, it’s not clear why anyone would use it. However, we hypothesized as a class that there may be other proofs elsewhere that show super-linear convergence, because many of us thought we had seen LBFGS listed as a super-linear algorithm. We’ll certainly look into this later as a class.

We spent time in class going over the secant condition that LBFGS, and BFGS, uses to approximate the Hessian. The key idea we had to understand is that the secant method can be viewed as a linear approximation of the Hessian analogous to making a linear approximation of the gradient by measuring the function value at two points. One measures the gradient at two locations $\nabla f(x)$ and $\nabla f(y)$ , and the secant condition is

$H(x - y) = \nabla f(x) - \nabla f(y)$ .

The BFGS method then iteratively projects the previous Hessian approximation onto the space of Hessian approximations that agree with this condition, which is reasonable if you believe the Hessian does not change much. LBFGS instead only stores the previous $m$ gradients and estimates the Hessian using those.

We also puzzled over how LBFGS can avoid the quadratic cost of either storing or computing the approximate Hessian. As a class, we were initially confused because most formulas for the approximate Hessian include outer product terms involving the differences between the input vectors and the gradients, e.g.,

$\underbrace{(x^{(j)} - x^{(j - 1)})}_{s^j} ~ \underbrace{(\nabla f(x^{(j)}) - \nabla f(x^{(j - 1)}))^\top}_{y_j}$ ,

where $s_j$ and $y_j$ are the shorthand used to describe these difference vectors in the slides. Based on the existence of these outer products, it appears as if an $O(n^2)$ cost is unavoidable, when all the literature says the memory and running time costs are $O(mn)$ .

The key insight to why we can avoid the quadratic cost—of even thinking about the full-sized Hessian—is that in all cases of these outer products, they are eventually right multiplied by yet another vector of length $n$ . We then have products of length- $n$ vectors that look like

$\underbrace{a b^\top}_{n \times n} \underbrace{c}_{n \times 1}$ ,

which can be computed much more efficiently by first multiplying the dot product on the right:

$\underbrace{a}_{n \times 1} \underbrace{b^\top c}_{1 \times 1}$ .

Concluding Thoughts

One of my goals with looking at these foundational methods first was to gain an intuition of how to prove convergence of more sophisticated optimization approaches. To do so, I was hoping to find nice patterns of proof techniques. I’m not certain that I did that, personally, with these three analyses. Parts of the analyses were analogous to each other, but overall, their convergence proofs seemed rather different to me. Perhaps as we see more analyses throughout the semester, we’ll start to recognize patterns more.

It’s interesting to have sat down to really dig into these methods, since so much of what I know as a machine learning researchers comes from “mythology” about these methods. One important note is the strength of the assumptions underlying the convergence guarantees. We often use these methods and variants on functions that may not be strongly convex or convex at all. These misuses of these algorithms will naturally occur. “When all you have is a hammer…” From spending three (and a half) classes looking at these convergence guarantees, I don’t yet have a clear idea of what we can say theoretically when these assumptions are violated.

Hello world!

This semester, I am teaching a graduate seminar course on optimization in machine learning. This blog will chronicle our exploration of the literature on this topic, including the results we find most interesting, the proof techniques that we want to highlight, and questions we have (whether because we couldn’t decipher the answer from the literature or because they are truly open questions). Most posts will be co-written by the students, but I’ll open with the first post on what we covered in the first few classes.