nnzhaocs

1. Lagrange dual problem: standard form, Lagrange dual function, and dual problem

First, we consider an optimization problem in the standard form:

minimize $f_{0}(x)$

subject to $f_{i}(x) \leq 0,$ i = 1, …, m

$h_{i}(x) \leq 0,$ i = 1, …, p

with variable $x \in R^{n}$ , domain $D = \bigcap_{i=0}^{m} dom f_{i} \cap \bigcap _{i=1}^{p} dom h_{i}$ is nonempty. The optimal value is $p^{*}$ .

The idea of lagrangian duality is to take the constraints into account by augmenting the objective function with a weighted sum of the constraint functions.

Lagrangian $L: R^{n}\times R^{m} \times R^{p}\rightarrow R$ as:
$L(x, \lambda , \nu ) = f_{0}(x)+ \sum_{i=1}^{m}\lambda _{i}f_{i}(x)+\sum_{i=1}^{p}\nu _{i}h_{i}(x),$

with $dom L = D \times R^{m}\times R^{p}$ , $\lambda _{i}$ as the Lagrange multiplier associated with the $i_{th}$ inequality constraint $f_{i}(x) \leq 0$ and $\nu_{i}$ as the Lagrange multiplier associated with the $i_{th}$ equality constraint $h_{i}(x) = 0$ .

Lagrange dual function is the minimum value of the Lagrangian.

For $\lambda \in R_{m}, \nu \in R_{p}$
$g(\lambda, \nu) = inf_{x \in D} L(x, \lambda, \nu) = inf_{x \in D}(f_{0}(x) + \lambda _{i}f_{i}(x)+\sum_{i=1}^{p}\nu _{i}h_{i}(x))$

If $\lambda \geq 0$ , then $g(\lambda, \nu) \leq p^{*}$ .

Proof:

If $x\hat{~}$ is feasible and $\lambda \geq 0$ , then
$f_{0}(x\hat{~}) \geq L(x\hat{~}, \lambda, \nu) \geq inf_{x\in D}L(x, \lambda , \nu) = g(\lambda , \nu)$
minimizing over all feasible $x\hat{~}$ gives $p^{*} \geq g(\lambda , \nu)$

The dual problem: what is the best lower bound that can be obtained from the Lagrange dual function?

maximize $g(\lambda , \nu)$
subject to $\lambda \geq 0$
Optimal value is denoted as $d^{*}$

2. Weak and strong duality

If $d^{*} \leq p^{*}$ , this property is called weak duality. The weak duality inequality holds when $d^{*}$ and $d^{*}$ are infinite while If the equality $d^{*} = p^{*}$ holds then we say that strong duality holds.

3. Geometric interpretation of dual function and lower bound $g(\lambda) \leq p^{*}$

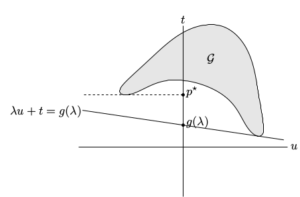
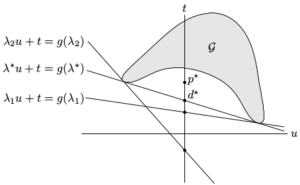
For a problem with one (inequality) constraint. Given λ, we minimize $( \lambda, 1)^{T}(\mu, t)$ over $G =\{(f _{1} (x), f _{0} (x)) | x \in D\}$ . This yields a supporting hyperplane with slope −λ. The intersection of this hyperplane with the u = 0 axis gives g(λ). Supporting hyperplanes corresponding to three dual feasible values of λ, i.e, optimum $\lambda ^{\ast }$ , $\lambda ^{1 }$ , and $\lambda ^{2 }$ . As shown in the figures, strong duality does not hold so the optimal duality gap $p^{\ast }-d^{\ast }$ is positive.

4. Price or profit interpretation

Suppose the variable x denotes how an enterprise operates and $f_{0}(x)$ denotes the cost of operating at x, then $-f_{0}(x)$ is the profit made at the operating condition x.

Each constraint $f_{i}(x) \leq 0$ represents some limit on resources (e.g., warehouse space, labor) or a regulatory limit (e.g., environmental). The operating condition that maximizes profit while respecting the limits can be found by solving the problem:

minimize $f_{0}(x)$

subject to $f_{i}(x) \leq 0$ , i = 1, …, m.

The resulting optimal profit is $- p ^{*}$ resulting optimal profit is $- p ^{*}$ .

Now imagine a second scenario in which the limits can be violated, by paying an additional cost which is linear in the amount of violation, measured by $f_{i}$ . Enterprise for the $i^{th}$ limit or constraint is $\lambda _{i}f_{i}(x)$ . Payments are also made to the firm for constraints that are not tight; if $f_{i}(x) \leq 0$ represents a payment to the firm.

The coefficient $\lambda _{i}$ has the interpretation of the price for violating $f_{i}(x) \leq 0$ ; its units are dollars per unit violation. For the same price the enterprise can sell any ‘unused’ portion of the $i^{th}$ constraint. We assume $\lambda _{i} \leq 0$ , i.e., the firm must pay for violations.

Reference

Boyd and Vandenberghe, Chapter 5–5.5 https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf