Author: youlu1

Phd student at Virginia Tech majoring in Computer Science.

Linear Convergence of the Primal-Dual Gradient Method for Convex-Concave Saddle Point Problems without Strong Convexity

Introduction

The convex-concave saddle point problem has the following format:

For many machine learning applications, their objective functions can be written in the convex-concave format. The example applications include reinforcement learning, empirical risk minimization and robust optimization etc.

We can use the following primal-dual gradient method to optimize the L(x,y).

In this paper, the authors develop a new method to prove that the primal-dual gradient method has linear convergence rate, when the f  and g  are smooth, f  is convex, g is strongly convex and the coupling matrix A has full column rank(Section 3). They also extend the primal-dual method to the stochastic situation and propose the primal-dual stochastic variance reduced gradient(SVRG) method. They use the new method to prove that the primal-dual SVRG method also has linear converge rate(Section 4).

Preliminaries

Before we prove the convergence of the primal-dual method, we need some preliminaries. First, we need the definitions of smoothness and strong convexity.

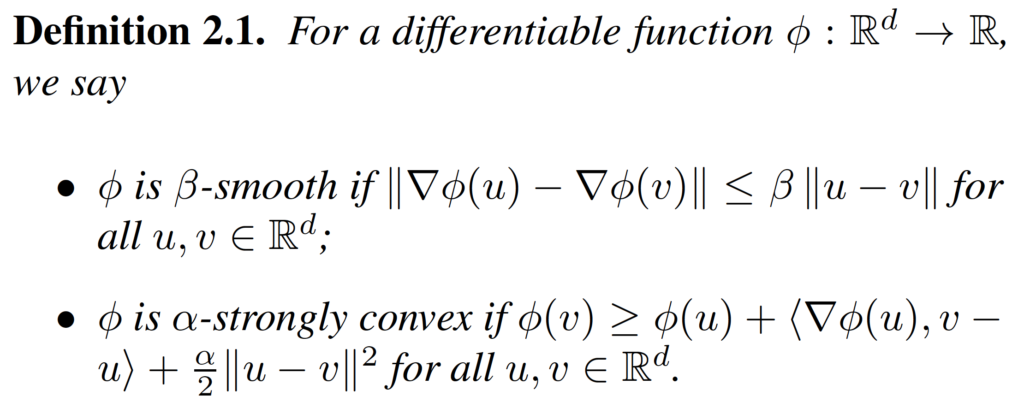
We also need the definition and some properties of  the conjugate function.

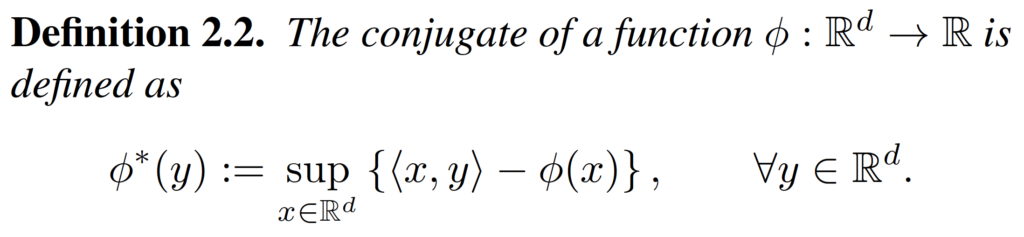
Based on the definition of conjugate function, we can get the corresponding primal problem of the L(x,y).

Finally, we need the of gradient descent on the strongly convex function.

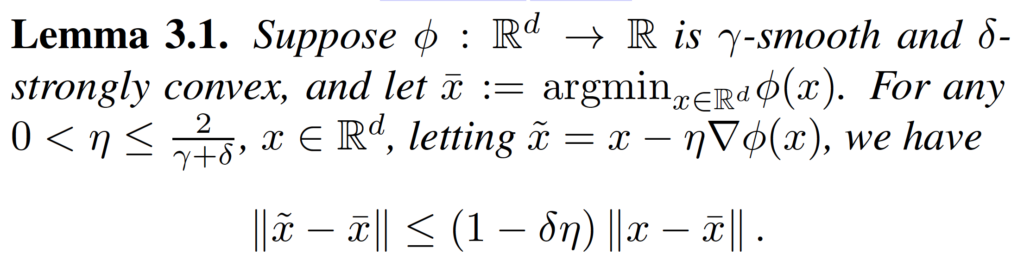
Linear Convergence of the Primal-Dual Gradient Method

With these preliminaries, we can start to prove the convergence of primal-dual gradient method. The Theorem 3.1 establishes the linear convergence guarantee for it.

This theorem says that if we construct a Lyapunov function P_t = \gamma a_t + b_t, we can prove that the function satisfies the condition that P_{t+1} \le (1-c)P_t, which implies the linear convergence rate.

We can divide the proof of this theorem to three steps. First, we bound the decrease of a_t. That is, we want to prove that a_{t+1} \le c_1 a_{t} + c_2 b_t. Second, we bound the decrease of b_t. Finally, we prove the inequality.

Proposition 3.1 and Proposition 3.2 give the bound of decrease of a_t.

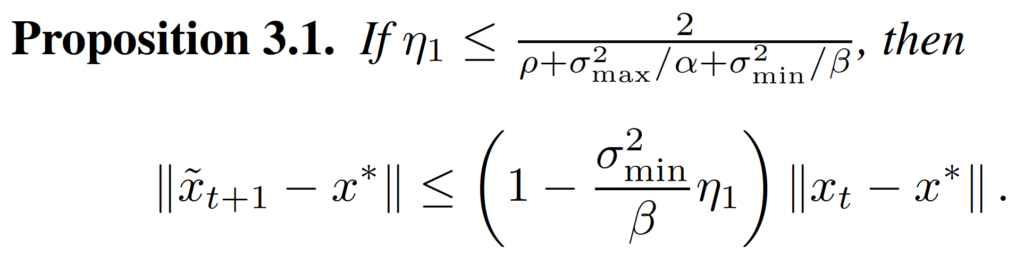
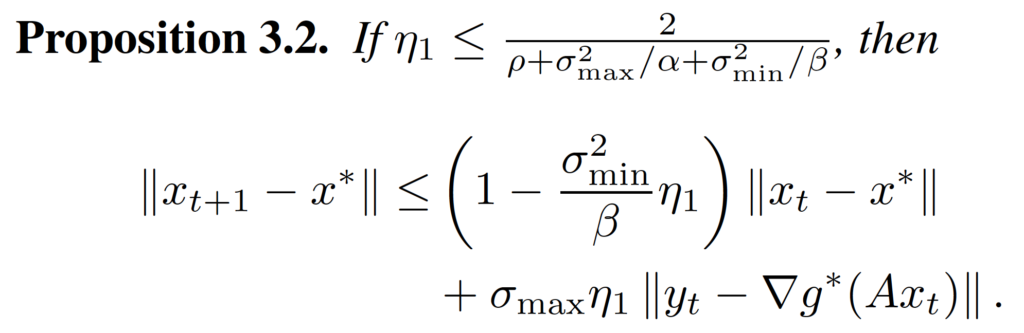
The proof technique of the first step is to first find the relationship between a_t and ||\tilde{x}_{t+1} - x^*||, and the relationship between x_{t+1} and \tilde{x}_{t+1}. And then use the triangle inequality to find the relationship among a_{t+1}, a_t and b_t. The authors call the \tilde{x}_{t+1} ghost variable in this paper, which is actually the $x$ obtained by updating the x_t with the true gradient, i.e., \nabla P(x).

Proposition 3.3 and Proposition 3.4 give the bound of decrease of b_t. We can use the convex function’s property to prove them.

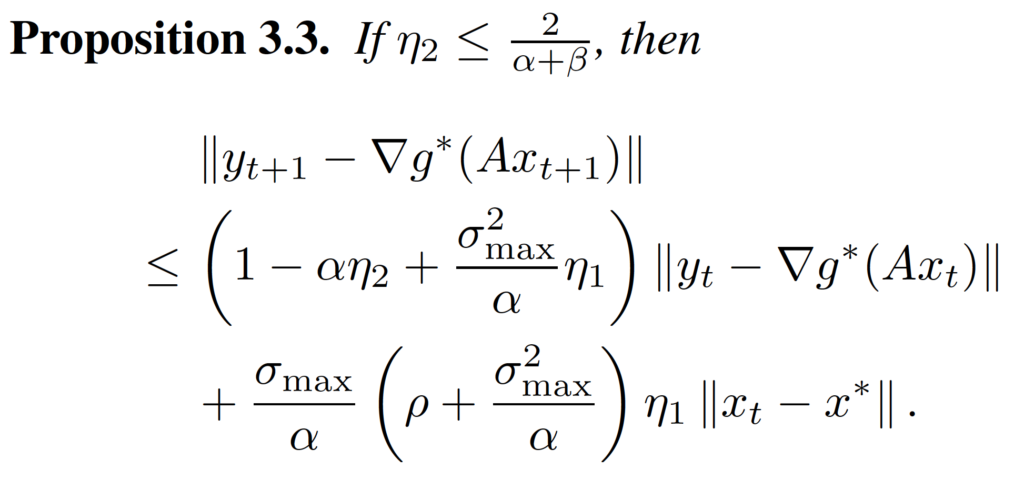
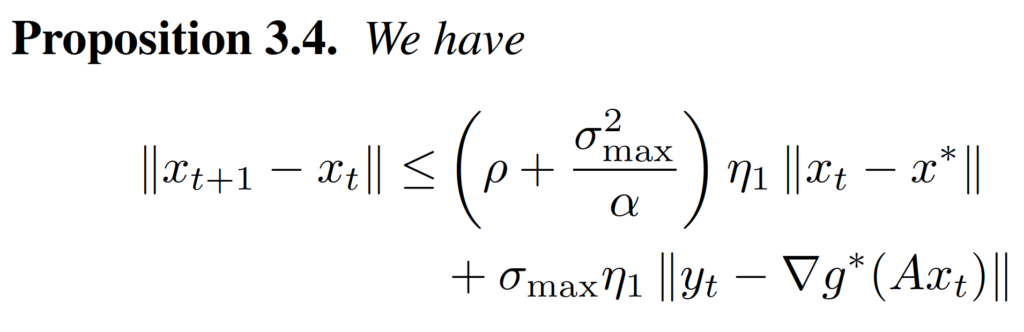
After we have these propositions, we can put them together, and with some routine calculations, we can prove the inequality in Theorem 3.1.

Extension to the Primal-Dual Stochastic Variance Reduced Gradient Method

In this section, the authors propose the primal-dual SVRG, and prove its convergence using the same proof method in the third section. The primal-dual SVRG is in Algorithm 2.

The framework of primal-dual SVRG is the same as the vanilla SVRG. The main difference is only that the primal-dual SVRG updates the parameters x and y together. In Theorem 4.1, they prove that the primal-dual SVRG also has the linear convergence rate.

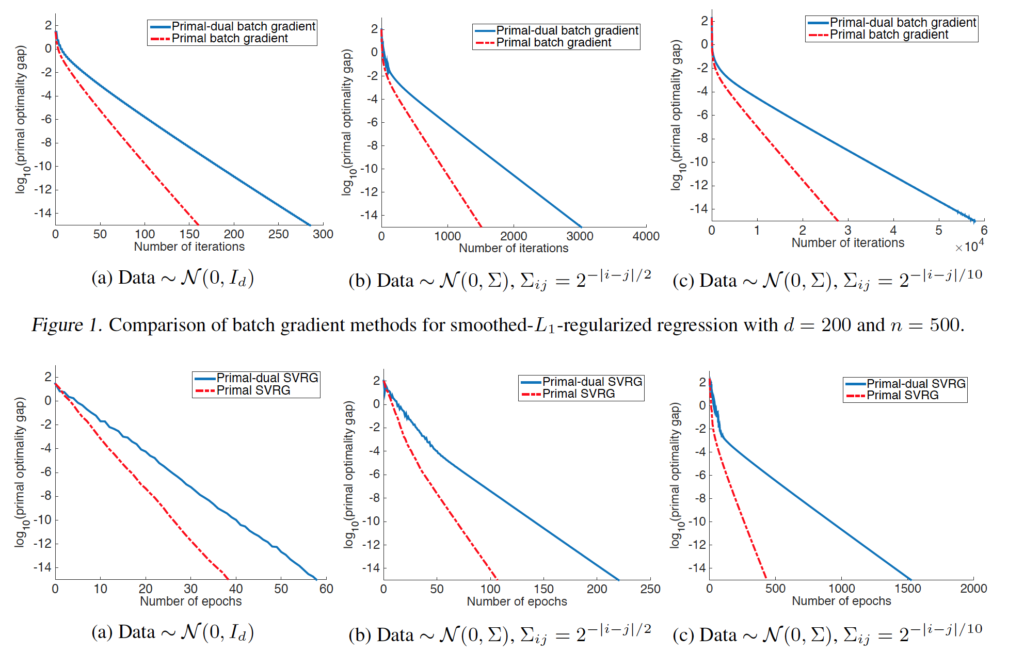
Preliminary Empirical Evaluation

They do experiments on synthetic dataset to prove the convergence of primal-dual gradient method. The results are as below.