Introduction
Standard machine learning approaches require centralizing the training data on one machine or in a datacenter. This work introduces an additional approach: Federated Learning, which leaves the training data distributed on the mobile devices, and learns a shared model by aggregating locally computed updates via a central coordinating server.
State-of-the-art optimization algorithms are typically inherently sequential. Moreover, they usually rely on performing a large number of very fast iterations. However, the round of communication is much more time-consuming than a single iteration of the algorithm, which lead to the development of novel algorithms specialized for distributed optimization.
Problem Formulation
This model proposed in this paper are considering the problem of minimizing an objection function that has the form of a sum, which is like this:
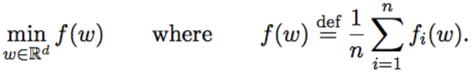
The examples for this kind of problem structure covers:
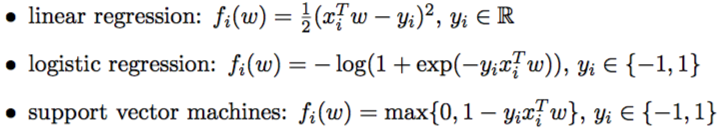
The Setting of Federated Optimization
Since communication efficiency is of utmost importance, algorithm for federated optimization follow the following characteristics.
Massively Distributed:
Data points are stored across a large number of nodes K. In particular, the number of nodes can be much bigger than the average number of training examples stored on a given node (n/K).
Non-IID:
Data on each node may be drawn from a different distribution; that is, the data points available locally are far from being a representative sample of the overall distribution.
Unbalanced:
Different nodes may vary by orders of magnitude in the number of training examples they hold.
Federated Learning
Federated Learning enables mobile phones to collaboratively learn a shared prediction model while keeping all the training data on device, decoupling the ability to do machine learning from the need to store the data in the cloud. This goes beyond the use of local models that make predictions on mobile devices by bringing model training to the device as well.
It works like this: your device downloads the current model, improves it by learning from data on your phone, and then summarizes the changes as a small focused update. Only this update to the model is sent to the cloud, using encrypted communication, where it is immediately averaged with other user updates to improve the shared model. All the training data remains on your device, and no individual updates are stored in the cloud.
Distributed settings and desirable algorithmic properties
We consider two distributed settings in this work. On a single machine, we compute the execution time as
where 
is the number of iterations algorithm A needs to converge to some fixed ε accuracy.
is the time needed for a single iteration.
On natural distributed machines, the execution time includes the communication overhead in a single iteration; c >> .
Desirable algorithmic properties for the non-IID, unbalanced, and massively-distributed setting are:
Property (A) is valuable in any optimization setting. Properties (B) and (C) are extreme cases of the federated optimization setting (non-IID, unbalanced, and sparse), whereas (D) is an extreme case of the classic distributed optimization setting (large amounts of IID data per machine). Thus, (D) is the least important property for algorithms in the federated optimization setting.
SVRG algorithm on a single node
The Central idea is the algorithm evaluates two stochastic gradients,∇fi(w) and ∇fi(wt) to estimate the change of the gradient of the entire function between points wt and w, namely ∇f(w)− ∇f(wt).
Under a distributed setting, we modify the objective as below:
The original problem formulation is 
If we define 
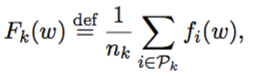then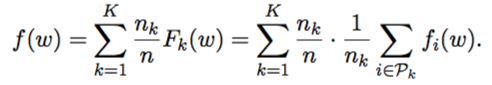 
Therefore, the objective is changed to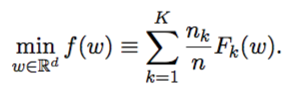
Distributed Approximate Newton algorithm (DANE)
The main idea of DANE is to form a local subproblem, dependent only on local data, and gradient of the entire function — which can be computed in a single round of communication.
Naive Federated SVRG
This proposition proves the effectiveness of the naive federated SVRG algorithm. However, this algorithm is inherently stochastic, and is valid under identical sequence of samples. This work further improves this algorithm to get the federated SVRG.
The Federated SVRG
The notations used in this work are summarized below:
Federated SVRG improves from naive federated SVRG from four parameters:
Since the local data sizes, nk, are not identical, so setting the stepsize hk inversely proportional to nk, making sure each node makes progress of roughly the same magnitude overall.
If K is more than 1, the values of Gk are in general biased estimates of ∇f(wt).
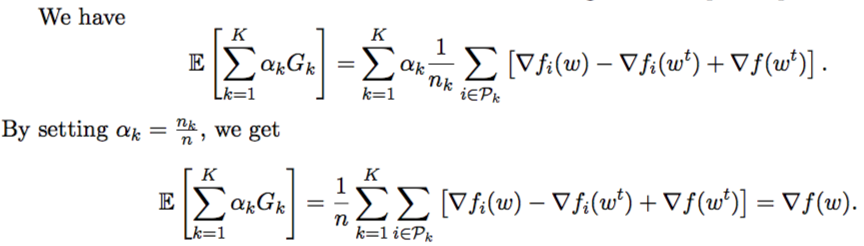
This motivates the aggregation of updates from nodes proportional to nk, the number of data points available locally.
Because of the un-even distribution of nonzeros for a particular feature,
repeatedly sampling and overshooting the magnitude of the gradient will likely cause the iterative process to diverge quickly. So we scale stochastic gradients by diagonal matrix Sk.
If a variable appears in data on each node, we are going to take average. However, the less nodes a particular variable appear on, the more we want to trust those few nodes in informing us about the meaningful update to this variable — or alternatively, take a longer step. Hence the per-variable scaling of aggregated updates.
Experiments
They provide results on a dataset based on public Google+ posts, clustered by user — simulating each user as a independent node.
The following figure shows the frequency of different features across nodes. In particular, over 88%
of features are present on fewer than 1000 nodes, which simulate the structure of distribution of the sparsity pattern.
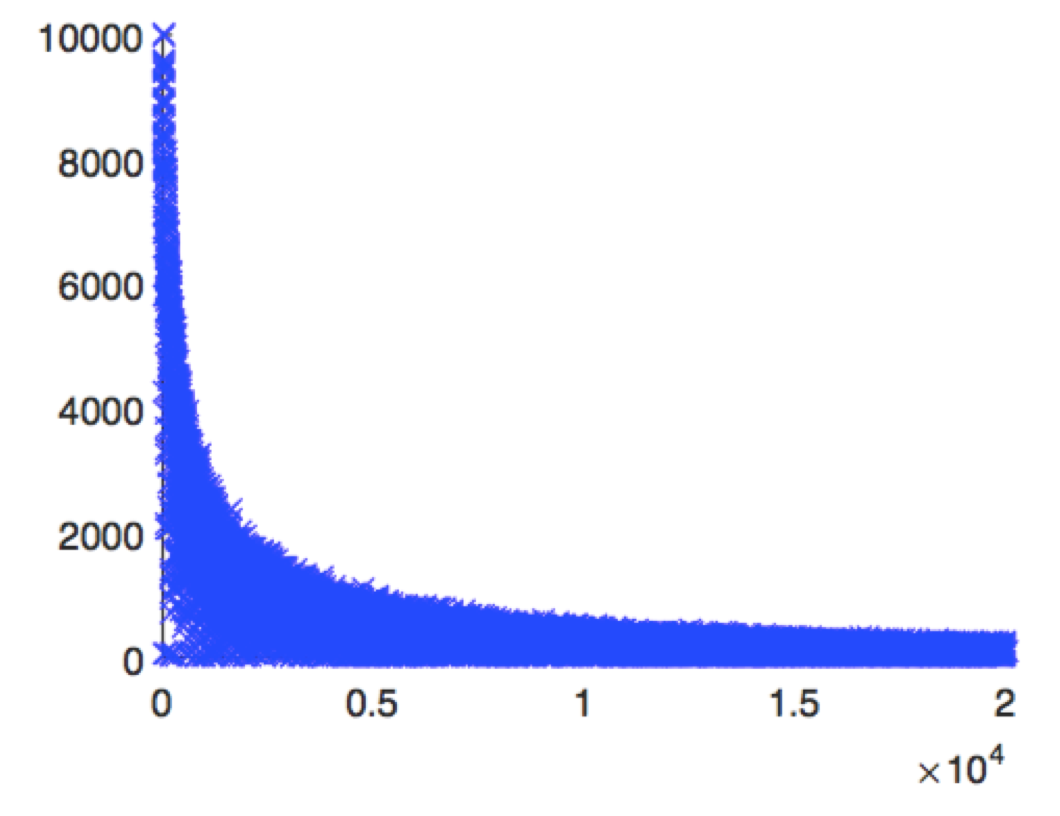
Figure 1: Features vs. appearance on nodes. The x-axis is a feature index, and they-axis represents the number of nodes where a given feature is present.
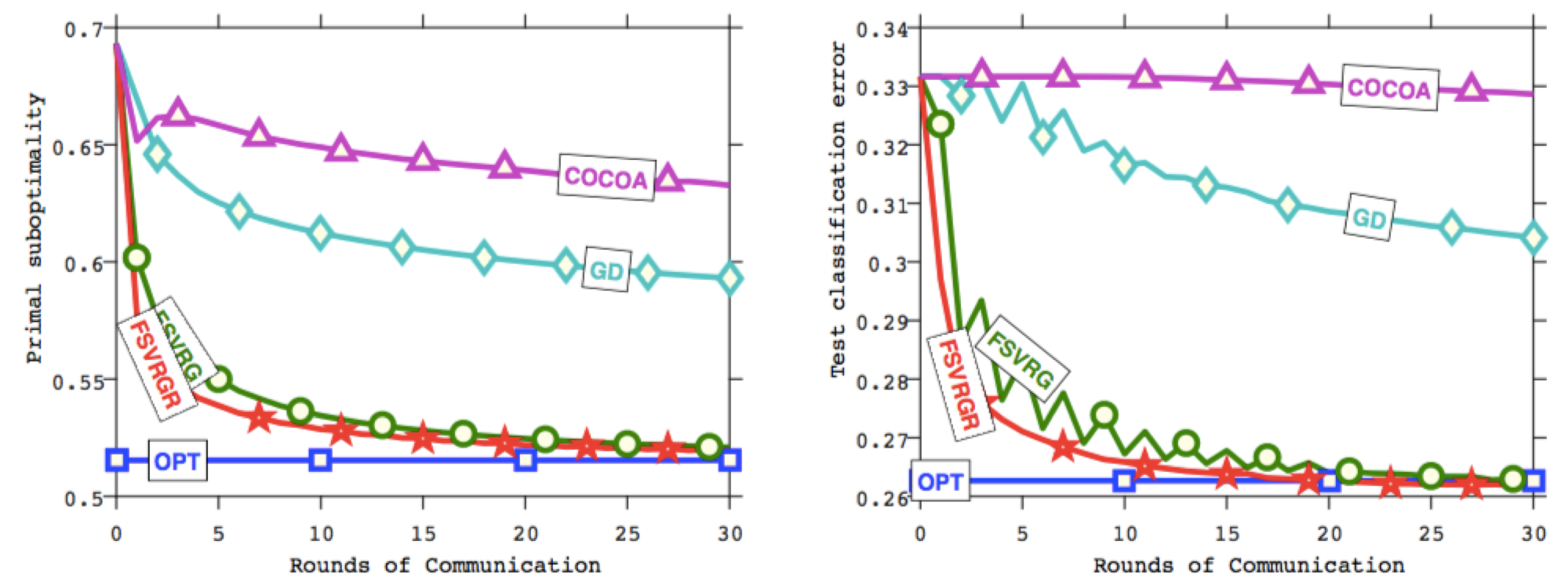
Figure 2: Rounds of communication vs. objective function (left) and test prediction error (right).
Figure2 show that FSVRG, converges to optimal test classification accuracy in just 30 iterations. Since the core reason other methods fail to converge is the non-IID data distribution, the experiment test the FSVRGR algorithm with data randomly reshuffled among the same number of nodes, which illustrate the algorithm is robust to challenges present in federated optimization.