Background – 1 Stochastic gradient descent
A dominant optimization algorithm for deep learning. While SDG finds minima that generalize well, each parameter update only takes a small step in later training period because the learning rate would be very small.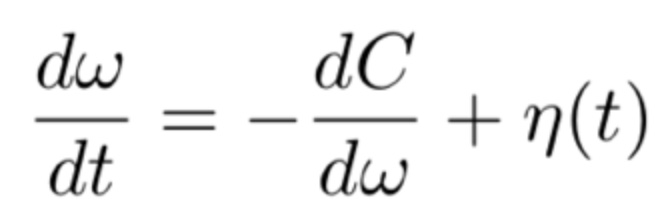
Background – 2 Previous work
Previous works declare an optimum fluctuation scale g that can be found to maximize the test set accuracy (at constant learning rate). They introduce an optimal batch size that B << N, so that g = epsilon(N/B -1) where B means batch size and N means training set size.
Background – 3 Large batch training
Instead of decay the learning rate to make the optimization function converge, there is another approach that to increase the batch size. The advantages are that it can reduce the number of paras updates required and can also be parallelized well and reduce training time. There is a backward that when batch size increase, the test set accuracy often falls a little bit.
Reference – 1 Industry need for the training algorithm
Jonathan Hseu, Google Brain Scientist, is introducing the algorithm time complexity tolerance.
Reference – 2 Existing training approach speed on GPU
Comparing to the existing work on GPU, this paper can train ResNet-50 on ImageNet to get 76.1% accuracy in 30 mins, by making the full use of the characteristic of TPU.
Main content – 1 Existed problem
When one decays the learning rate, one simultaneously decays the g. However, the learning rate is not the necessary factors to decays the g and make the function converge.
Main content – 2 Solution
Do increase the batch size during training instead of decaying the learning rate. When learning rate wants to drop by alpha, it increases the batch size by alpha.
Main content – 3 Advantage
First, This approach can achieve a near-identical model performance with the same number of training epochs. Second, it significantly reduces the parameter updates in the training process. Third, it doesn’t require any fine-tuning process.
Main content – 4 Further Enhancement
After achieving the same quality of result with the learning rate decay approach, the batch size increase approach is also able to further reduce the number of para updates by further increasing the learning rate, scaling B that proportional to epsilon or increasing the momentum coefficient and scale B that proportional to 1/(1-m).
Main content – 5 Consequent
It successfully trains an Inception-ResNet-V2 on ImageNet under 2500 para updates using batches of 65536 images and gets 77% accuracy. It successfully trains a ResNet-50 on ImageNet to 76.1% accuracy in 30 mins.
Main content – 6 Contribution
First, it shows the quantitative equivalence of increasing the batch size and decaying the learning rate. Second, it provides a straightforward pathway towards large batch training.
Result analysis – 1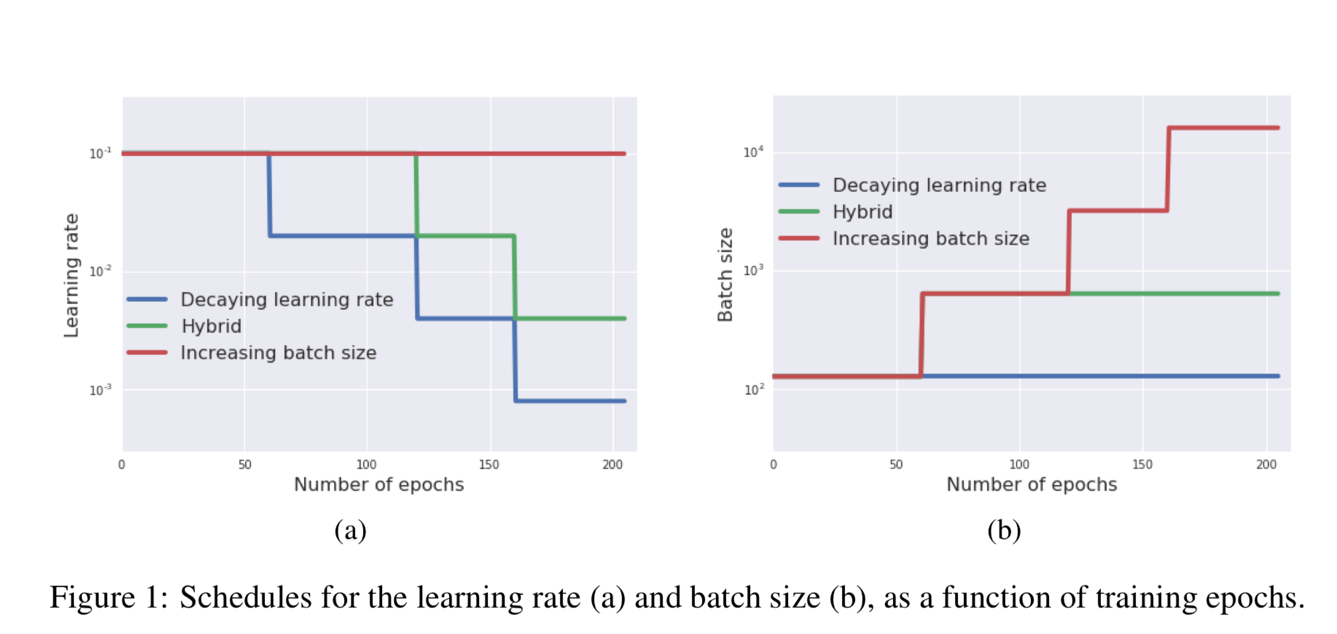
Figure 1 shows an example that how the learning rate and batch size change in the different algorithms. For the blue line decaying learning rate, the learning rate is reduced in the training process (number of epochs increase) but the batch size is always constant. For the red line increasing batch size, the batch size is increased in the training process (number of epochs increase) but the learning rate is always constant.
Result analysis – 2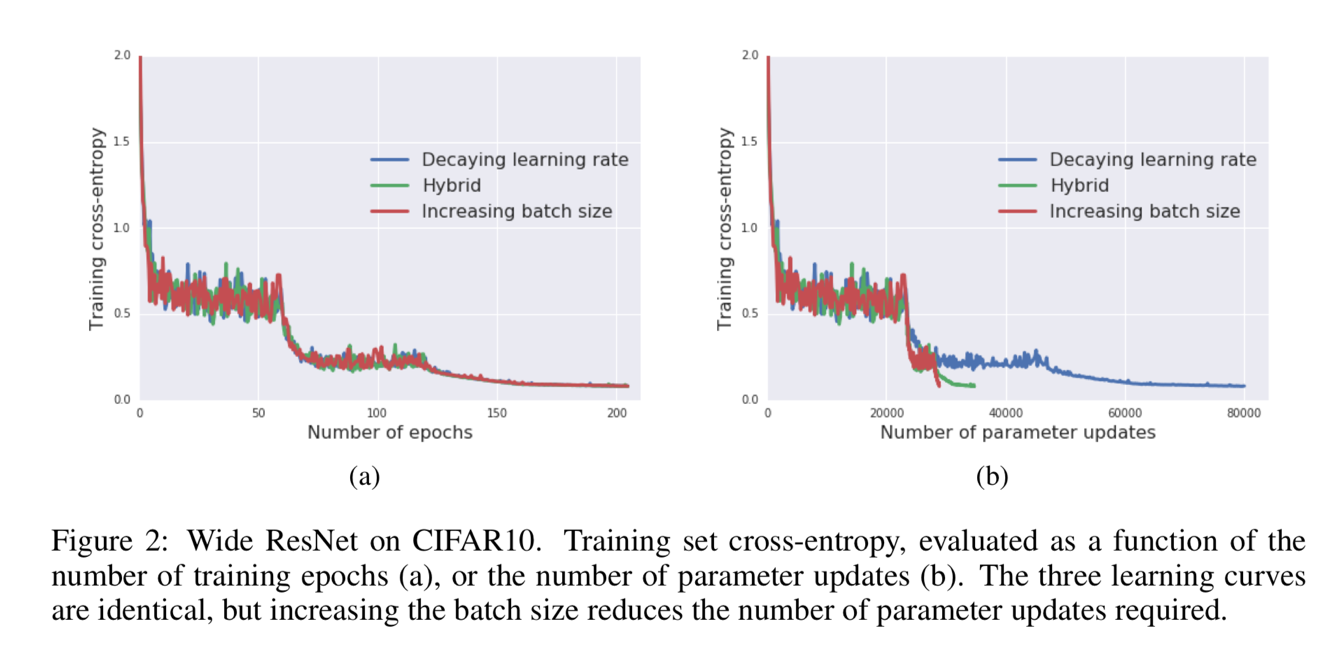
Figure 2 shows that the increasing batch size approach can achieve a qualitatively equivalent result than the decreasing learning rate approach. However, it only needs around 1/3 training updates.
Result analysis – 3 & 4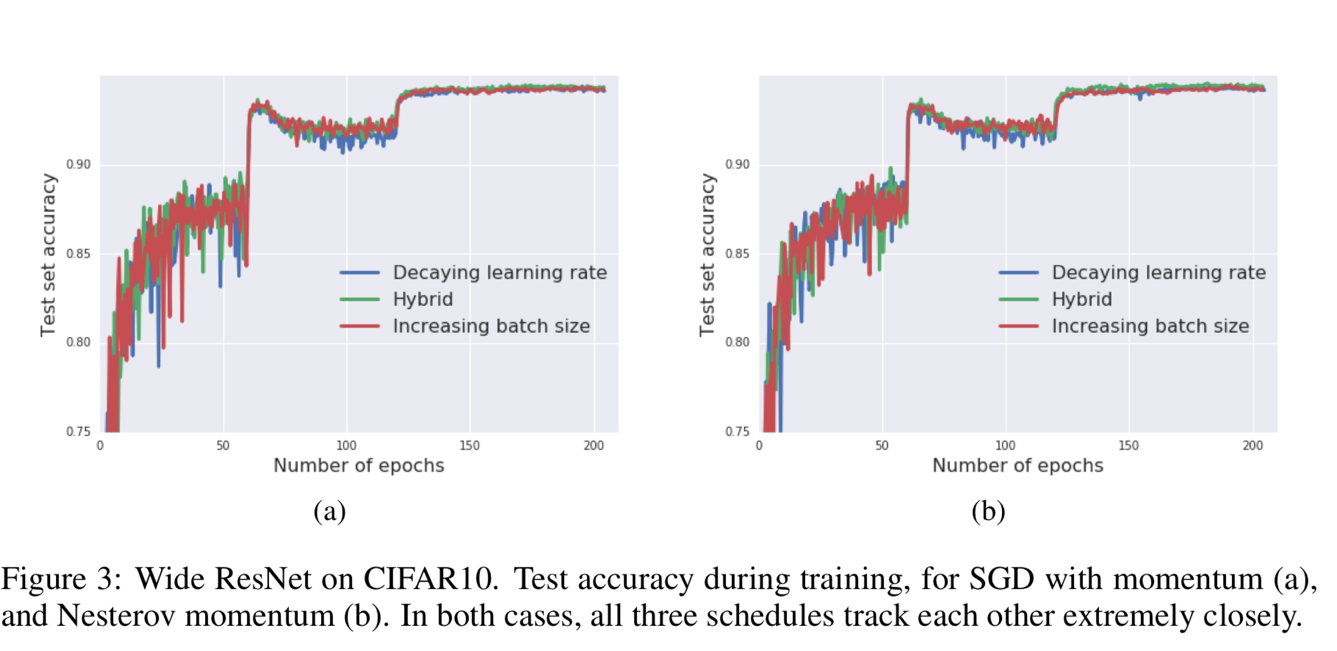
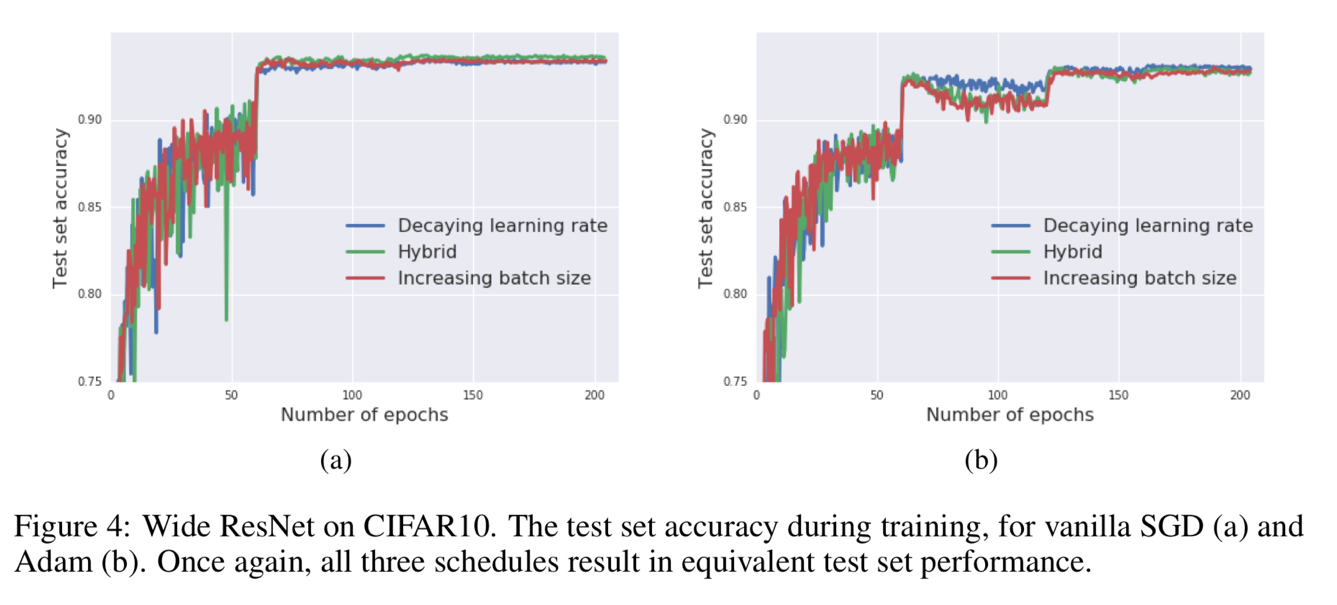Figure 3 and Figure 4 show that the batch size increasing approach can be applied to many different optimization algorithms, like SGD with momentum, Newterow momentum, vanilla SGD and Adam.
Result analysis – 5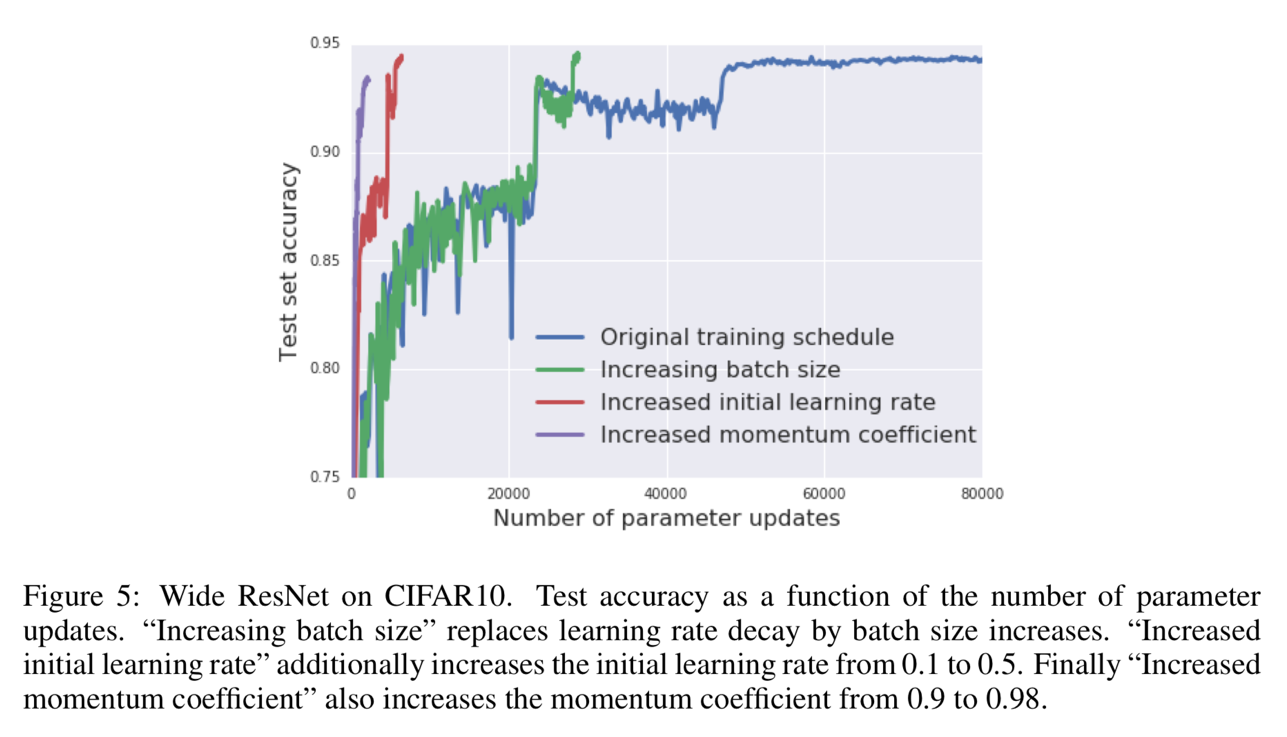
Figure 5 shows the truth that after achieving the same quality equivalent of result with the learning rate decay approach, the batch size increase approach is also able to reduce the number of para updates further. Blue: original learning rate decaying method; Green: batch size increasing method; Red: batch size increasing method + further increase initial learning rate; Purple: batch size increasing method + further increase initial learning rate + further increase momentum coefficient.
Result analysis – 6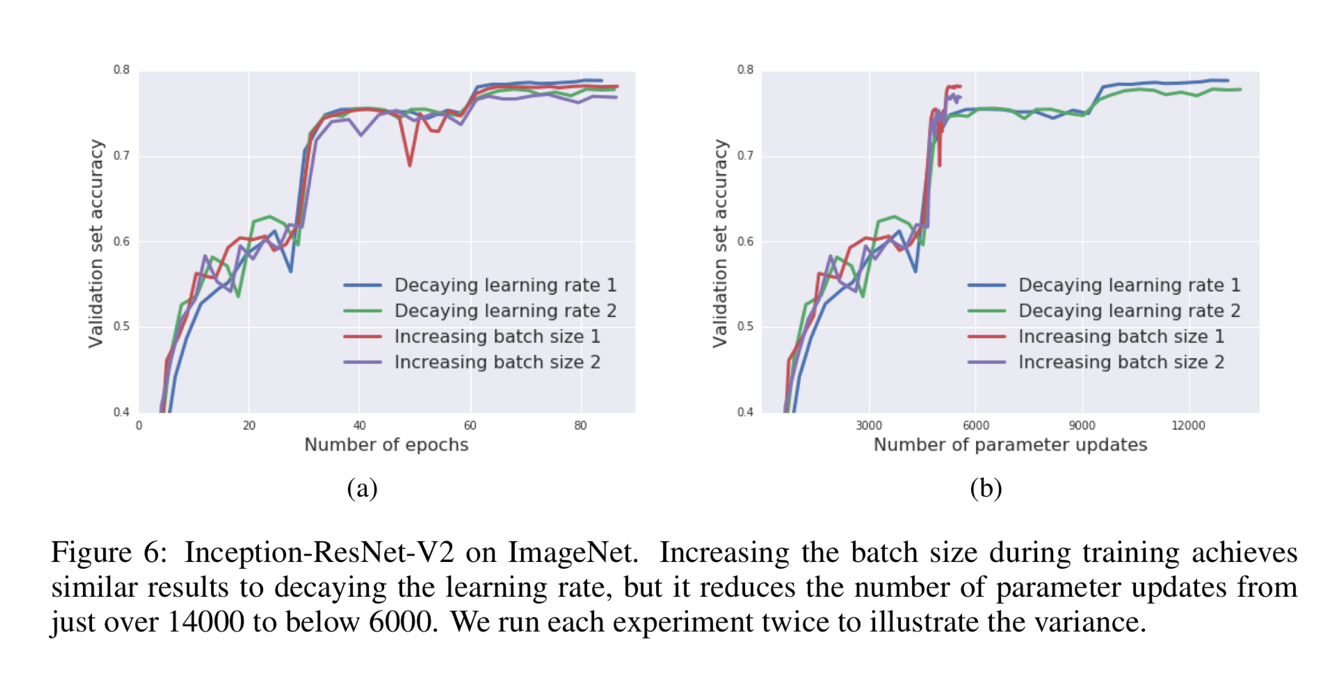
Figure 6 proves the validity and reproducibility of this algorithm by conducting the experiments many times.
Result analysis – 7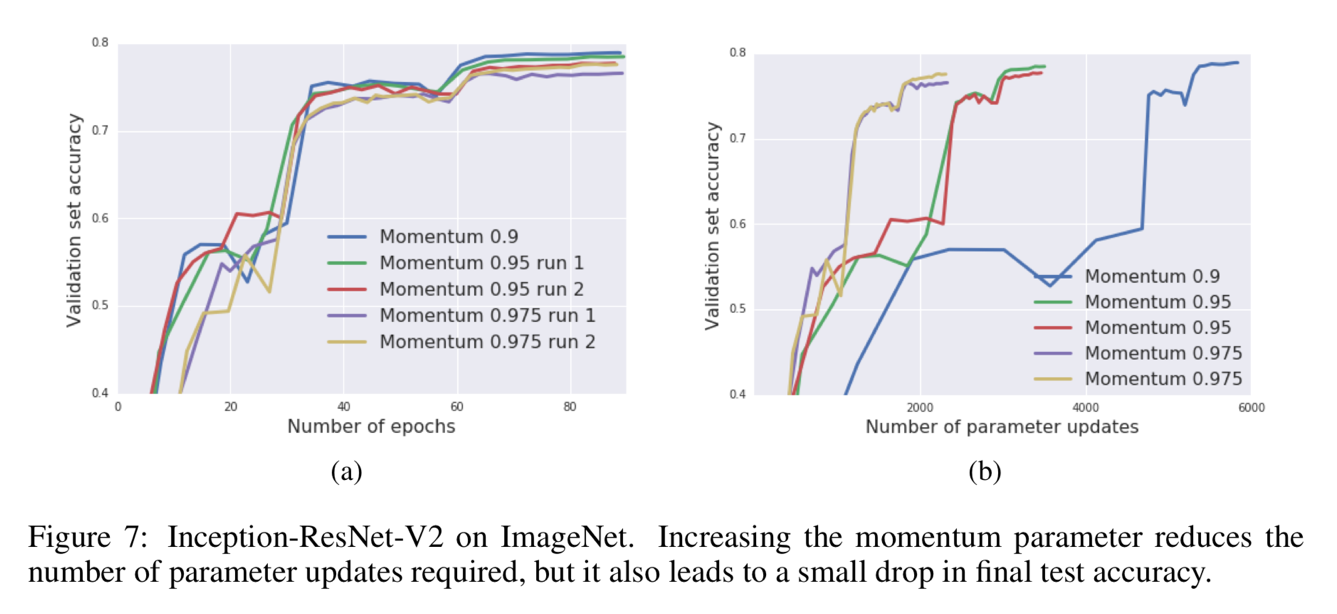
Figure 7 shows that the influence of momentum coefficient that increasing the momentum can reduce the update times as well as reduce the training time consuming but can let the accuracy fall a little bit.