maheshnm

Introduction

Proximal algorithms are a class of algorithms that can be used to solve constrained optimization problems that may involve non-smooth penalties in the objective function. Their formulation is rather general in that a number of other optimization algorithms can be derived as special cases of proximal algorithms. At the core of proximal algorithms exists the evaluation of the proximal operator:

$\textnormal{prox}_{\gamma, f} (x)= \textnormal{argmin}_{z} \left\{f(z) + \frac{1}{2\gamma} \left\|x-z\right\|^{2}_{2}\right\}$

The proximal operator returns a point in the search space that minimizes the problem defined by the Moreau envelope of the objective function $f$ [2]:

$f^{\gamma}(x) = \inf_{z} \left\{f(z) + \frac{1}{2\gamma} \left\|x-z\right\|^{2}_{2}\right\}$

The Moreau envelope is a regularized version of the function $f$ . It is continuously differentiable and defined in all of $\mathbb{R}^{n}$ , even though $f$ may not satisfy either condition, and has the same set of minimizers as $f$ [1,2].

Example 1. Let $f(x) = |x|$ . The Moreau envelope of $f(x)$ is $f^{\gamma}(x)$ and for $\gamma = 1$ :

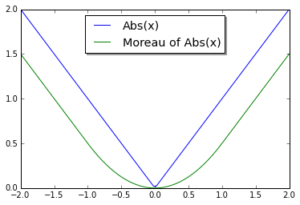
Notice that the Moreau envelope is smooth even though $f$ itself is not.

Standard Problem Formulation

Consider the minimization of functions of the form

$\textnormal{argmin}_{x \in \mathcal{X}}\, F(x) := g(x) + h(x)\qquad\qquad (1)$

where $g(x)$ is convex and differentiable and $h(x)$ is convex but non-smooth. Such objective functions arise when a penalty such as the lasso is added to the original objective function $g(x)$ to induce sparsity in the solution.

Gradient descent can be used to minimize the original objective $g(x)$ as it is smooth and convex, and we can converge to an $\epsilon$ -suboptimal solution at a rate of $O(1/\epsilon)$ . Adding a penalty or regularization term $h(x)$ that is non-smooth, however, may cause gradient descent to fail and converge to an incorrect minima. In such a circumstance, subgradient methods [3] are used to minimize the non-smooth function $F(x)$ . The drawback of using subgradient methods is that they converge far more slowly than gradient descent. An $\epsilon$ -suboptimal solution can be obtained only after $O(1/\epsilon^2)$ iterations.

When the solution to the proximal operator of $h(x)$ is known in closed form, proximal algorithms can be used to significantly speed up the convergence. Table 1 in [2] lists the closed form solution of evaluating the proximal operator on an extensive list of non-smooth functions. Convergence to the an $\epsilon$ -suboptimal solution can be attained after $O(1/\epsilon)$ calls to evaluate the prox operator. Therefore, if the evaluation of the prox operator is cheap, convergence is linear as in the case of gradient descent.

Proximal Gradient Descent Method

Proximal gradient descent method can be employed to solve optimization problems of type (1). It is composed of the following two steps:

Gradient step: Starting at $x_k$ , take a step in the direction of the gradient of the differentiable part, $g(x)$ :
$x_{k}^{+} = x_{k} - \gamma \nabla g(x_k)$
Evaluate prox operator: Starting at $x_k^{+}$ , evaluate the prox operator of the non-smooth part, $h(x)$ :
$x_{k+1} = \textnormal{prox}_{\gamma, h}(x_{k}^{+}) = \textnormal{prox}_{\gamma, h}(x_k - \gamma \nabla g(x_k))$

In [2], the authors give a glimpse into how the above recipe can be motivated in two different ways — first as an MM-algorithm and second by deriving optimality conditions using subdifferential calculus.

Proximal Gradient Descent method will require $O(1/\epsilon)$ calls to the prox operator in order to obtain an $\epsilon$ -suboptimal solution.

Proximal Newton Method

In Proximal Gradient Descent Method, the gradient step is obtained by constructing a quadratic under-approximant to the differentiable function using the scaled identity, $I/\gamma$ , as an approximation to the Hessian of $g(x)$ .

Proximal Newton Method can be obtained by using the actual Hessian, $H := \nabla^{2}g(x)$ , to build the quadratic under-approximant of $g(x)$ . Since $g(x)$ is convex, $H \succeq 0$ . Defining the scaled proximal map as in [4]:

$\textnormal{prox}_{H}(x) = \textnormal{argmin}_{z} \frac{1}{2}\left\|x-z\right\|^{2}_{H} + h(x)$

where $\left\|x\right\|^{2}_{H} = x^{T}Hx$ , the Proximal Newton Method can be written as [4]:

Newton step: Starting at $x_k$ , take a Newton step:
$x_{k}^{+} = x_{k} - H_{k}^{-1} \nabla g(x_k)$
Evaluate prox operator: Starting at $x_k^{+}$ , evaluate the scaled prox operator:
$z_{k} = \textnormal{prox}_{H_{k}}(x_{k}^{+}) = \textnormal{prox}_{H_{k}}(x_{k} - H_{k}^{-1} \nabla g(x_k))$
Take a step in direction $(z^{k} - x^{k})$ : Starting at $x_k$ , evaluate $x_{k+1}$ as:
$x_{k+1} = x_{k} + t_{k} (z_{k} - x_{k})$

It should be noted that the the proximal operator in the case of Proximal Newton Method relies on the computation of the Hessian. Hence, any line search strategy to identify an appropriate step size will prove expensive.

Proximal Gradient Descent Method can be recovered from Proximal Newton Method by replacing the Hessian with $H = I/\gamma$ . Whereas the Proximal Gradient Descent Method converges linearly, Proximal Newton Method shows local quadratic convergence [4].

Nesterov Acceleration

Nesterov suggests that the optimal convergence rate for first order methods is $O(1/\sqrt{\epsilon})$ in [6]. In [5], he introduces ideas to accelerate convergence of smooth functions and shows that the optimal rate is achievable. Accelerated Proximal Gradient Descent Method is built upon the foundations of the ideas laid in [6]. The method is structured as follows [4]:

Choose initial point: $x_{-1} = x_{0} \in \mathbb{R}^{n}$
Compute an intermediate vector $x_{k-1}^{+}$ : Starting at $x_{k-2}$ and $x_{k-1}$ , evaluate:
$x_{k-1}^{+} = x_{k-1} + \frac{k-2}{k+1} \left(x_{k - 1} - x_{k - 2}\right)$
Evaluate the prox operator after taking a gradient step using $x_{k-1}^{+}$ : Starting at $x_{k-1}^{+}$ , evaluate $x_{k}$ as:
$x_{k} = \textnormal{prox}_{t_k, h}(x_{k-1}^{+} - t_{k} \nabla g(x_{k-1}^{+}))$

The intepretation of

$x_{k-1}^{+} = x_{k-1} + \frac{k-2}{k+1} \left(x_{k - 1} - x_{k - 2}\right)$

is the same as momentum. If $h(x) \equiv 0$ , then the prox operator is identity and accelerated gradient descent method is recovered [4].

Summary

Proximal algorithms can be used to solve constrained optimization problems that can be split into sum of convex differentiable and convex non-smooth parts. If the prox operator is cheap to evaluate, then linear convergence is recovered in the usual scenario, like in the case of gradient descent. Several other algorithms can be recast in terms of a proximal method [1,2]. Although closed form solutions to prox operator may be required, in [7] the authors study the convergence rates when the prox operator is evaluated in an inexact manner.

References

[1] Parikh, N. and Boyd, S., 2014. Proximal algorithms. Foundations and Trends® in Optimization, 1(3), pp.127-239. [paper]

[2] Polson, N.G., Scott, J.G. and Willard, B.T., 2015. Proximal algorithms in statistics and machine learning. Statistical Science, 30(4), pp.559-581. [paper]

[3] Boyd, S., Xiao, L. and Mutapcic, A., 2003. Subgradient methods. lecture notes of EE392o, Stanford University, Autumn Quarter, 2004, pp.2004-2005. [monograph]

[4] Tibshirani, R., 2016. Proximal Newton Method. Slides from 10-725, Carnegie Mellon University, Fall , 2016. [presentation]

[5] Nesterov, Y., 1983, February. A method of solving a convex programming problem with convergence rate O (1/k2). In Soviet Mathematics Doklady (Vol. 27, No. 2, pp. 372-376). [paper]

[6] Nesterov, Y., 2013. Introductory lectures on convex optimization: A basic course (Vol. 87). Springer Science & Business Media. [book]

[7] Schmidt, M., Roux, N.L. and Bach, F.R., 2011. Convergence rates of inexact proximal-gradient methods for convex optimization. In Advances in neural information processing systems (pp. 1458-1466). [paper]

Author: maheshnm

Proximal Algorithms