Learning to learn by gradient descent by gradient descent

Introduction

Tasks in ML are typically defined as finding a minimizer of an objective function $f(\theta)$ over some domain $\theta \in \Theta$ . The minimization itself is performed using gradient descent -based methods, where the parameters are updated taking into account the gradient information. $\theta_{t+1} = \theta_{t} - \alpha_{t} \nabla f(\theta_{t})$ . Many optimizations have been proposed over the years which try to improve the descent-based methods by incorporating various techniques utilizing the geometry , adaptive learning rates, momentum .

The paper approaches the optimization from a novel perspective: using learned update rules for our network, capable of generalizing to a specific class of problems. The update to the current set of parameters is predicted by a neural-network, specifically RNN-based network ( $\theta_{t+1} = \theta_{t} + g_{t}$ ).

Framework

Given an Optimizee: $f(\theta)$ parameterized by $\theta$ and Optimizer $f(\phi)$ parameterized by $\phi$ .

The objective function for the optimizer is

$L(\phi) = \mathop{\mathbb{E}}_{f}{ \lbrack \sum_{t=1}^{T} w_{t} f(\theta_{t}) \rbrack }$

where $\theta_{t+1} = \theta_{t} + g_{t}$

and $g_t , h_{t+1} = m( \nabla_{t} , h_{t}, \phi)$ .

The update steps $ latex g_{t}$ and next hidden state $h_{t+1}$ are the output of the recurrent neural network architecture parameterized by $\phi$ .

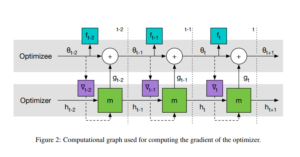
$w_{t} \in R_{\leq 0}$ are weights associated with the predicted values of the optimizee for the last t time steps. $w_{t} =1$ value is used in all the experiments. The optimizee parameters are updated with truncated back-propagation through time. The gradient flow can be seen in the computational graph below. The gradients along the dashed lines are ignored in order to avoid computing expensive second-derivative calculation.

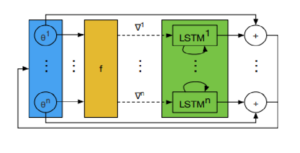
Coordinatewise LSTM architecture

Applying per-parameter different LSTM would have been computationally very expensive and would have introduced more than tens/thousands of parameters to optimize on.
To avoid this issue, this paper utilizes a coordinatewise network architecture (LSTM-based architecture) where the optimizer parameters are shared over different parameters of the optimizee and separate hidden state is maintained for each optimizee parameter. The base LSTM architecture is a two-layer LSTM using standard forget-gate architecture.

Preprocessing

One key difficulty when passing the gradients of parameters to the optimizer network is how to handle the different scales of the gradients. Typical deep networks work well when the input to the network is not arbitrarily-scaled.

Instead of passing the gradient $\nabla$ directly, $(\log \nabla, sgn(\nabla) )$ the logarithm of the gradients and the sign of the gradients to the RNN architecture is passed to the coordinatewise architecture.

Experiment

The authors used 2 layer LSTMs with 20 hidden units in each layer for optimizer. Each optimizer is trained by minimizing the loss equation using truncated BPTT. Adam with the learning rate chosen by random line search is used for minimization. The authors compare the trained optimizers with standard optimizers like SGD, RMSProp, ADAM and NAG. The learning rate for these optimizers are tuned while the other parameters are set to default values in Torch7.

The authors evaluated a class of 10 dimensional synthetic quadratic functions whose minimizing function is in form:

where W is a 10X10 matrix and y is 10 dimensional vector drawn from IID Guassian distribution. As shown in the fig below LSTM based optimizer performs much better than the standard optimizers.

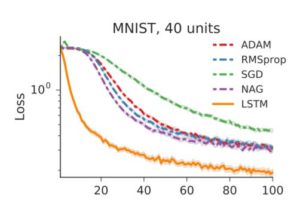
The author has trained optimizer over a neural network with 1 hidden layer of 20 hidden units using sigmoid activation on MNIST training set. They have experimentally shown that the optimizer generalizes much better than standard optimizers for different architectures with more layers (2) and hidden units (40) as shown below.

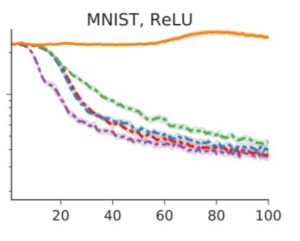
However, when the architecture is changed drastically like using relu activation instead of Sigmoid, the LSTM optimizer does not scale well as shown below.

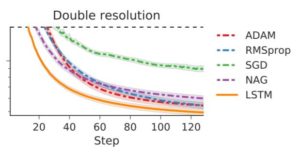
The author has used LSTM optimizer for neural art to generate multiple image styles using 1 style image and 1800 content images. They found that LSTM optimizer outperform standard optimizers for test content images at training resolution as well as twice the training resolution as shown below.

Conclusion

The authors have shown how to cast the design of optimization algorithms as learning problems. Their experiments have shown that learnt neural optimizers perform better than state of art optimizers for deep learning.

References

[1] Learning to Learn by gradient descent by gradient descent( https://arxiv.org/abs/1606.04474)