A Bayesian Perspective On Generalization And Stochastic Gradient Descent. Part 2

Section 4. Bayes Theorem and Stochastic Gradient Descent

In section 4, the main idea is about the idea “Bayesian principles account for the generalization gap”:

1. The test set accuracy often falls as the SGD batch size is increased (holding all other hyper-parameters constant).
2. Since the gradient drives the SGD towards deep minima, while noise drives the SGD towards broad minima.
3. Expect the test set performance to show a peak at an optimal batch size, which balances these competing contributions to the evidence.

To evaluate the idea that there is the “generalization gap”, they used a shallow neural network with 800 hidden units and RELU hidden activations, trained on MNIST without regularization. They use SGD with a momentum parameter of 0.9. They use a constant learning rate of 1.0 which does not depend on the batch size or decay during training. The model trained on just 1000 images, selected at random from the MNIST training set. This enables us to compare small batch to full batch training.

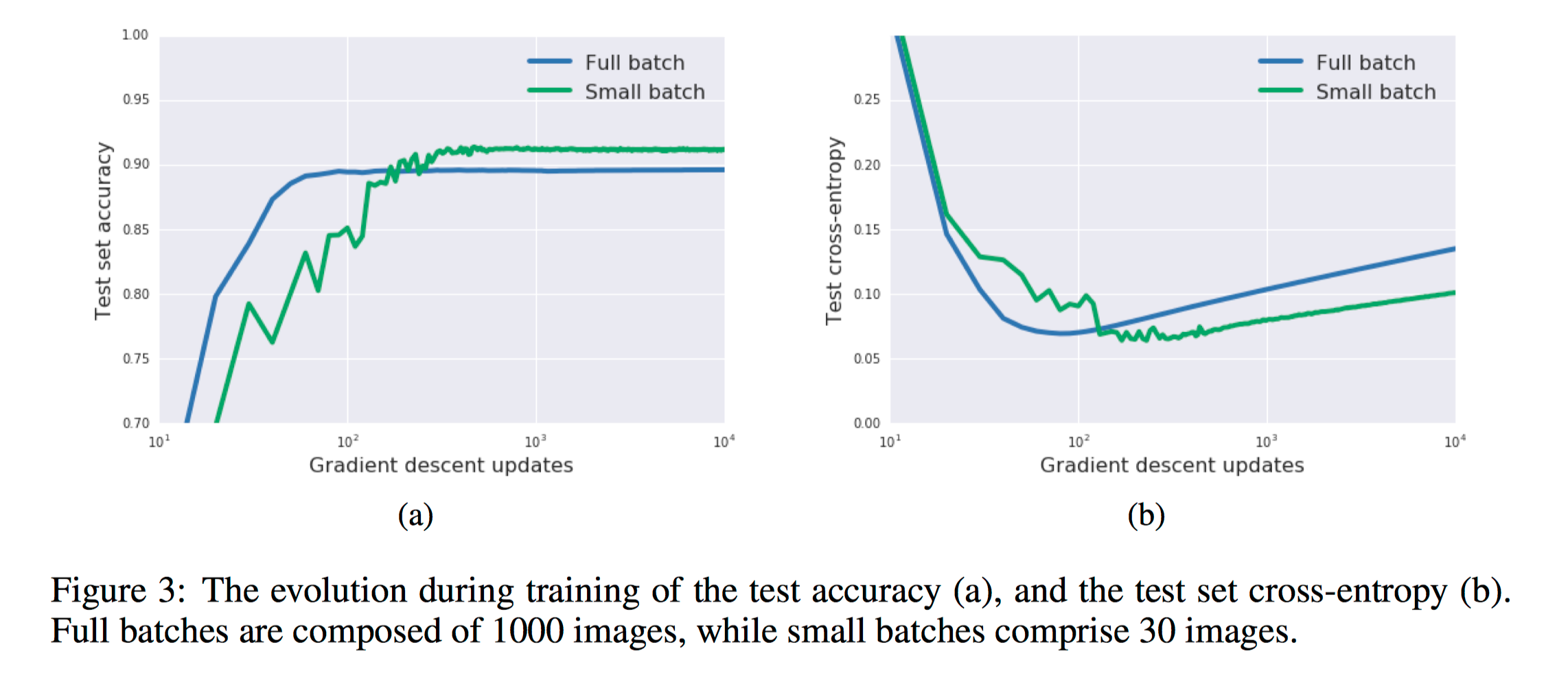
In figure 3, they exhibit the evolution of the test accuracy and test cross-entropy during training. Our small batches are composed of 30 images, randomly sampled from the training set. Looking first at figure 3a, small batch training takes longer to converge, but after a thousand gradient updates a clear generalization gap in model accuracy emerges between small and large training batches.

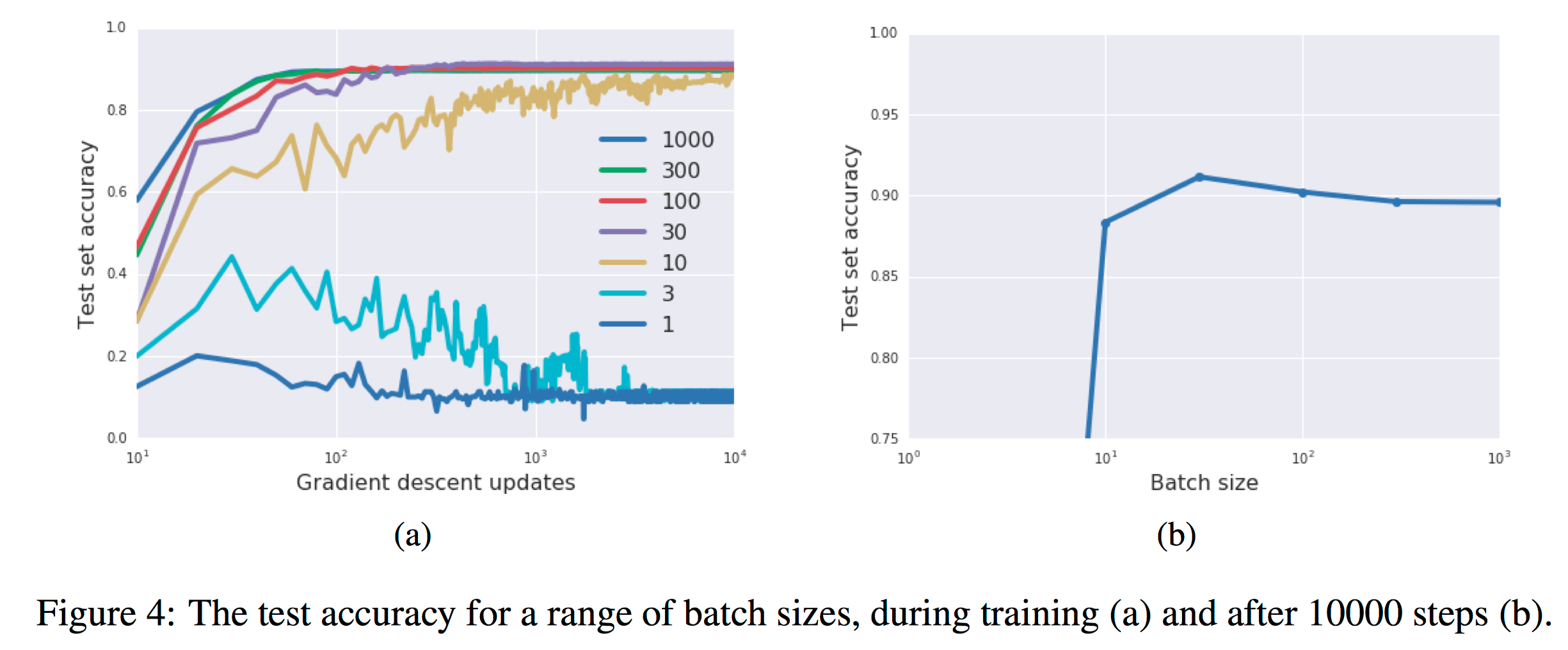In figure 4a, they exhibit training curves for a range of batch sizes between 1 and 1000. They find that the model cannot train when the batch size B less than 10. In figure 4b they plot the mean test set accuracy after 10000 training steps. A clear peak emerges, indicating that there is indeed an optimum batch size which maximizes the test accuracy, consistent with Bayesian intuition.

Section 5. STOCHASTIC DIFFERENTIAL EQUATIONS AND THE SCALING RULES

Based on the above evaluation, they conclude that:

1. The test accuracy peaks at an optimal batch size, if one holds the other SGD hyper-parameters constant.
2. The authors argued that this peak arises from the tradeoff between depth and breadth in the Bayesian evidence.
3. However it is not the batch size itself which controls this tradeoff, but the underlying scale of random fluctuations in the SGD dynamics.
4. They now identify this SGD “noise scale”, and use it to derive three scaling rules which predict how the optimal batch size depends on the learning rate, training set size, and momentum coefficient.

To get the relationship between noise scale and other four parameters: “Bach size, Learning rate, training set size and Momentum coefficients”. Based on the following states, we could get the relationships as between:

1. Central limit theorem:

2. Model the gradient error with Gaussian random noise:

3. Stochastic differential equation:

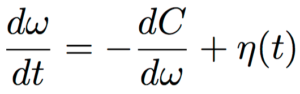
Based on these above three rules, we get:

The noise scale falls when the batch size increases, consistent with our earlier observation of an optimal batch size Bopt while holding the other hyper-parameters fixed. Notice that one would equivalently observe an optimal learning rate if one held the batch size constant. When we vary the learning rate or the training set size, we should keep the noise scale fixed, which implies:

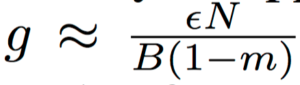
This scaling rule allows us to increase the learning rate with no loss in test accuracy and no increase in computational cost, simply by simultaneously increasing the batch size. We can then exploit increased parallelism across multiple GPUs, reducing model training times.

In figure 5a, the authors plot the test accuracy as a function of batch size after (10000/) training steps, for a range of learning rates. Exactly as predicted, the peak moves to the right as increases. In figure 5b, they plot the best-observed batch size as a function of learning rate, observing a clear linear trend. The error bars indicate the distance from the best-observed batch size to the next batch size sampled in our experiments.

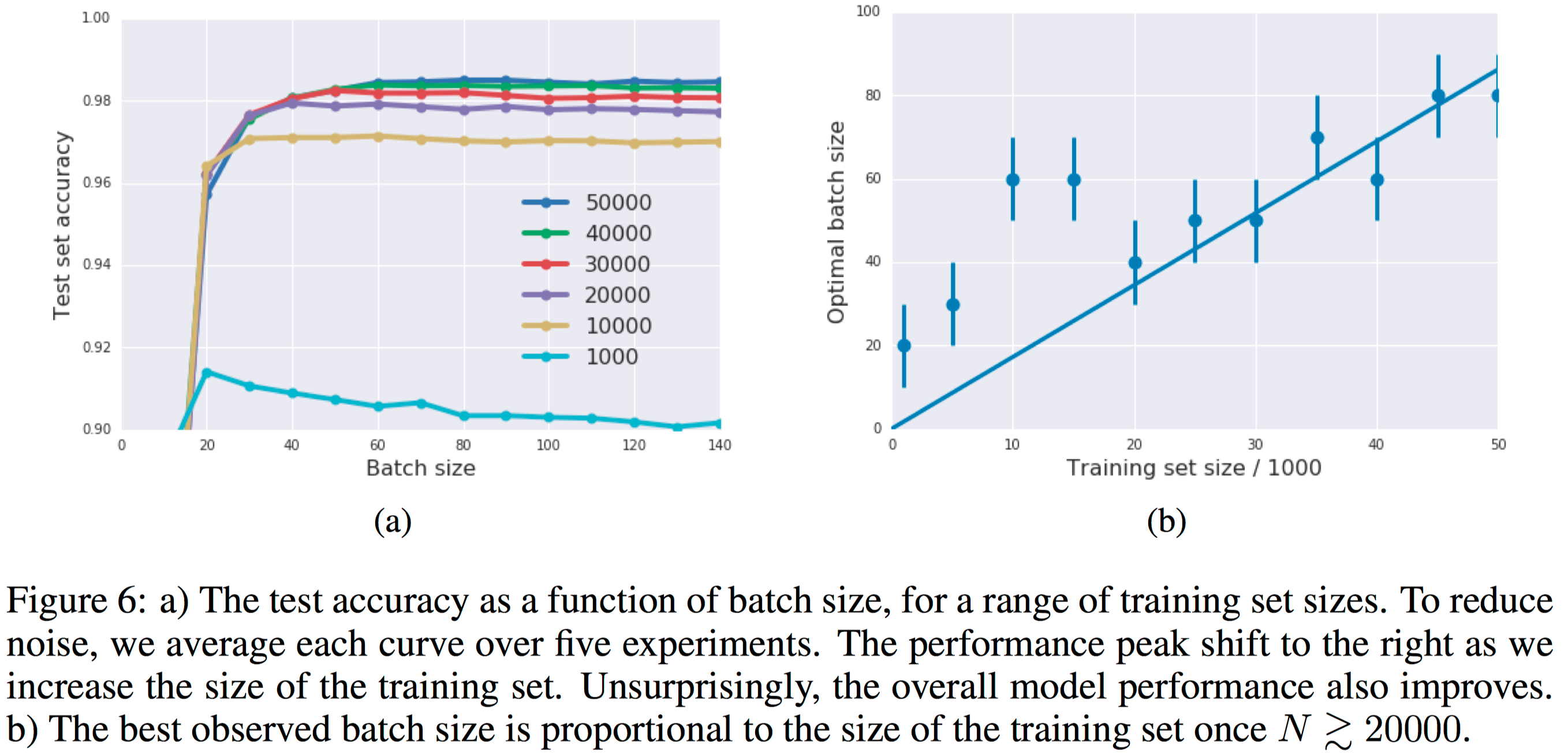
In figure 6a they exhibit the test set accuracy as a function of batch size, for a range of training set sizes after 10000 steps. Once again, the peak shifts right as the training set size rises, although the generalization gap becomes less pronounced as the training set size increases.

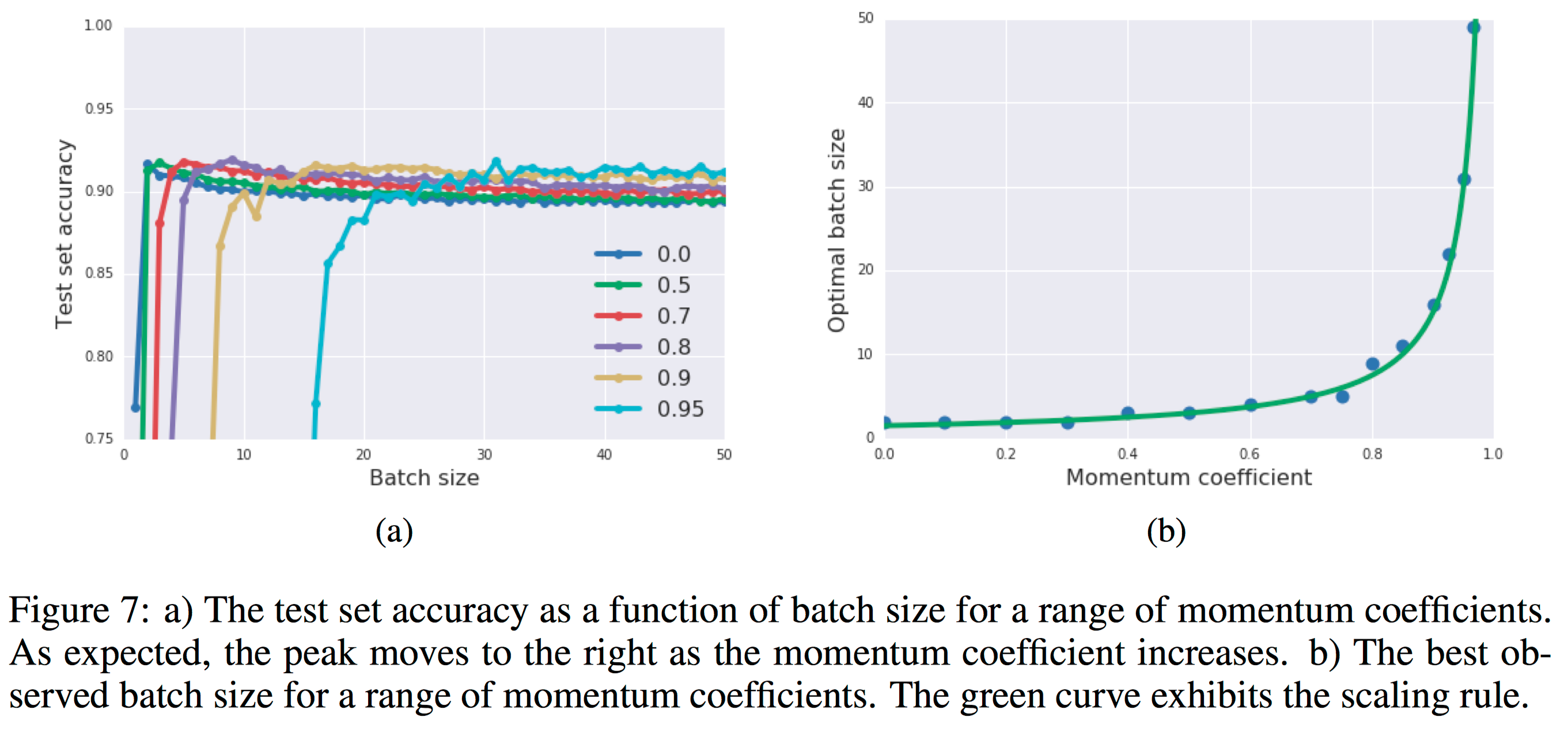
In figure 7a, they plot the test set performance as a function of batch size after 10000 gradient updates, for a range of momentum coefficients. In figure 7b, the authors’ plot best-observed batch size as a function of the momentum coefficient, and fit our results to the scaling rule above; obtaining remarkably good agreement. We propose a simple heuristic for tuning the batch size, learning rate and momentum coefficient.